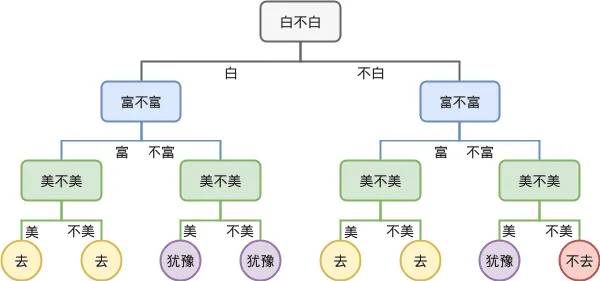
机器学习之决策树

熵

熵（Entropy），在本文中是指信息熵（Information
Entropy），简单的来说，就是指一件事情的不确定性的度量，其单位为（Bit）。相对的，信息的单位也是Bit，刚好是信息熵的反义词，是指一件事情的确定性。

首先，引入熵的计算公式：
$$
Ent(D) = - \sum_k^{| \mathcal{Y} |} P_k log_2{P_k}
\tag{1}
$$

假如，有一道单项选择题，拥有$A、B、C、D$四个选项，小明不会做，所以说，对于小明来说，这四个选项的正确概率都是25%，即：

选项	正确概率
$A$	$25%$
$B$	$25%$
$C$	$25%$
$D$	$25%$

故，此时，对于小明来说，这道题的熵为：
$$
Det(题目) = - \sum_{k=1}^4 25% * \log_2 {25%} = 2
$$
所以说，对于小明来说，这道题的熵为2bit。

其中熵的定义公式中出现了几个变量与概念：

• $\mathcal{Y}$ ： 是指结果中出现的可能性情况，这些可能性被称作是微观态，如：抛掷一枚硬币的微观态为2中，抛掷两枚硬币的微观态为4中。这道题中，微观态是4种。
• $P_k$：每种微观态发生的可能性，我们用$P_k$的倒数来模拟微观态发生的次数。

当小红告诉小明，选项$C$的正确率为$50%$时（假设小红告诉小明的是真实信息），发生了什么？微观态状态变化为下表：

选项	正确概率
$A$	$16.6%$
$B$	$16.6%$
$C$	$50%$
$D$	$16.6%$

此时的信息熵为：
$$
Det(题目) = - 3 \times 16.6% * log_2(16.6%) - 50% * log_2(50%) = 1.79
$$
由此可见，熵减小了，所以，小红告诉小明的这条信息的大小为$2-1.79 = 0.21bit$。

如果说，小红告诉小明，选项D是错的。那么：

选项	正确概率
$A$	$25%$
$B$	$25%$
$C$	$50%$
$D$	$0%$

此时的信息熵为：
$$
Det(题目) = - 2 \times 25% * log_2(25%) - 50% * log_2(50%) = 1.04
$$
此时，小红告诉小明的这条信息大小为$1.79-1.04=0.75bit$。

条件熵

条件熵是指：如果$H(Y| X = x)$为变量$Y$在变量$X$取特定值$x$条件下的熵，name$H(Y|X)$就是$H(Y|X)$在$X$取遍所有可能的$x$后，取平均的结果。

给定随机变量$X$与$Y$， 定义分别为$\mathcal{X}$与$\mathcal{Y}$，在给定$X$条件下，$Y$的条件熵。

$$
\begin{align}
H(X|Y) & = \sum_{x \in \mathcal{X}} p(Y|X=x) \\
& = - \sum_{x \in \mathcal{X}} p(x) \sum_{x \in \mathcal{Y}} p(y|x) \log p(y | x) \\
& = - \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y) \log p(y|x) \\
& = - \sum_{x \in \mathcal{x}, y \in \mathcal{Y}} p(x,y) \log p(y|x) \\
& = - \sum_{x \in \mathcal{x}, y \in \mathcal{Y}} p(x,y) \log \frac{p(x,y)}{p(x)} \\
& = \sum_{x \in \mathcal{x}, y \in \mathcal{Y}} p(x,y) \log \frac{p(x)}{p(x,y)} \\
\end{align}
$$

信息增益

信息增益是指：信息获取之后，熵减小的量。

如果一条信息的信息增益为0，则这条信息被称作噪音或者噪声。对于整个系统是一条没有意义的信息。

信息增益的计算方法为：
$$
Gain(D, a) = Det(D) - Det(D, a)
\tag{2}
$$
直观的理解就是：信息增益是未获取信息时的熵减去获取信息后的熵。

ID3.5算法

ID3.5 算法主要包含以下步骤。

• 计算所有样本的关于分类指标的熵
• 依次添加样本特征后计算出每个熵，选取信息增益最大的特征，将样本划分为不同的子树，该处，子树的个数与样本的微观态种类数有关。
• 在子树中继续进行以上两个操作。知道特征都使用完成或者决策树的深度达到要求。

C4.5算法

C4.5算法中引入了一个特别的概念。

信息增益率：

$$
\begin{align}
GainRatio(D, A) & = \frac{Gain(D,A)}{SlitInformation(D,A)}
\\
& = \frac{Gain(D,A)}{- \sum _{i=1} ^\mathcal{Y} \frac{|D_i|}{D} \log_2 \frac{|D_i|}{D}}
\end{align}
\tag{3}

$$

C4.5算法其实就是将ID3.5算法中的熵，换成了信息增益率。这样做的好处有一个，就是：

• ID3.5算法中，如果某一个特征的样本数数量要比其他特征的样本数多很多。那么他在ID3.5算法中会有很高的权值。
• C4.5算法中，信息增益率的分母其实就是将信息增益按照其样本数量缩放了，解决了上述问题。
• 但是C4.5算法中却恰恰相反，对于某个特征的样本数比较少的情况，会有更高的权值。

CART算法与基尼(Gini)指数

基尼指数的计算公式：
$$
\begin{align}
Gini(D, A) & = \sum_{i}^{|\mathcal{Y}|}P_k(1-P_k)
\\
& = \sum_{i}^{|\mathcal{Y}|} (P_k - P_k^2)
\\
& = 1- \sum_{i}^{|\mathcal{Y}|}P_k^2
\end{align}
\tag{4}
$$

基尼指数是指，在样本中，某个特征的均匀度（不纯度）的度量。如果一个样本中，某个特征分布的越不均匀，那么其基尼指数就越大。

那么我们就可以用基尼指数来代替信息熵和信息增益率，进行算法的计算。这就是CART（$Classification\ And\ Regression\ Tree$）算法。