SVM原始形式推导
欧式空间平面的常见性质
证明$\omega$是平面的法向量
$$
\left \lbrace
\begin{matrix}
\omega^T\mathcal{x_1} + b = 0 \\
\omega^T \mathcal{x_2} + b = 0
\end{matrix}
\right .
\to \omega^T(\mathcal{x_1} - \mathcal{x_2}) = 0 \to \omega^T \mathcal{x} = 0
\tag{1}
$$
点到平面的距离
$$
\begin{align}
r & = || \frac{\omega^T x}{||\omega||^2} \omega - \frac{-b}{ ||\omega || ^2} \omega || \\
& = ||\frac{\omega^Tx}{||\omega||^2} + \frac{-b}{||\omega||^2}|| \cdot||\omega|| \\
& = \frac{|| \omega^Tx + b ||}{||\omega||} \\
& = \frac{|\omega^T x + b|}{||\omega||}
\end{align}
\tag{2}
$$
西瓜书中的$6.2$式
SVM原始形式的导出
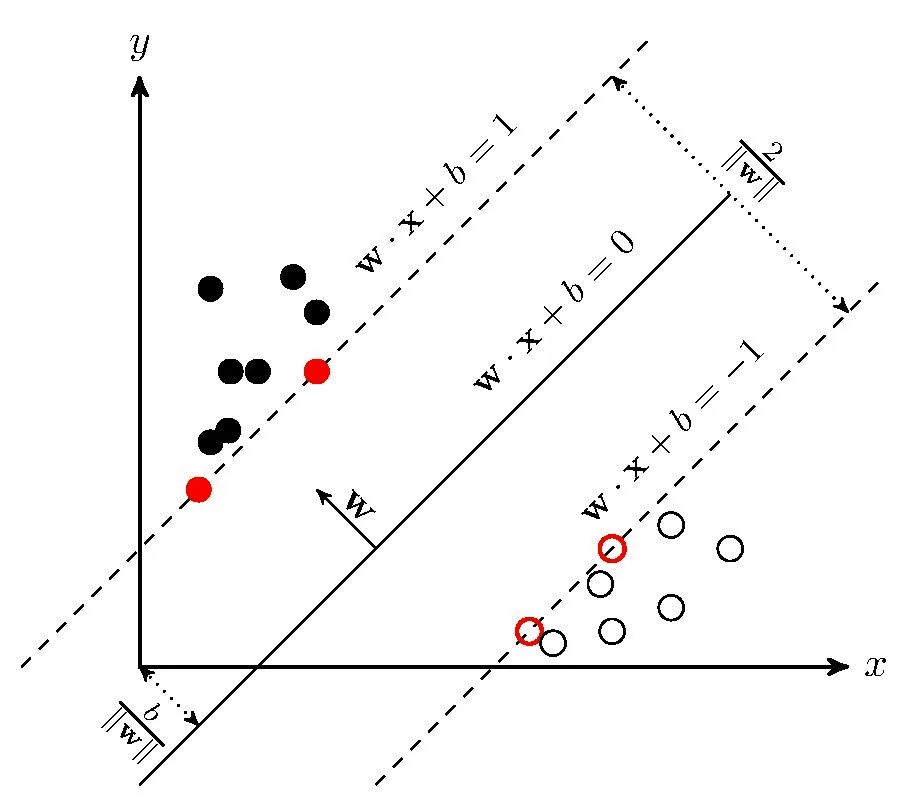
核心是最大化间隔
我们设有样本$y_i$是已经能够被正确分割开的正样本和负样本,则:
$$
r_i = \frac{y_i(\omega^Tx_i + b)}{||\omega||}
\tag{3}
$$
就可以将$(2)$式中的绝对值号去掉了(方便求导)。
则,我们最终需要求取的就是离平面最近的一个点,所以需要求取:
$$
d = \min_i y_i \left( \frac{\omega ^T x}{||\omega||} + \frac{b}{||\omega||} \right)
\tag{4}
$$
接着,我们还需要调整超平面的位置,使得其离最近的样本点的距离(所谓间隔)是最大的:
$$
d^* = \max_{\omega, b} d = \max_{\omega, b} \min_i y_i \left( \frac{\omega ^T x}{||\omega||} + \frac{b}{||\omega||}
\right)
\tag{5}
$$
其中,我们可以将$d^*$与$r$的关系表述为下:
$$
\mathcal{r} = 2d^* = \max_{\omega, b} d = \max_{\omega, b} \min_i 2 \times y_i \left( \frac{\omega^T x}{||\omega||} +
\frac{b}{||\omega||} \right )
\tag{6}
$$
所有可能的距离之中,最大的距离是间隔的一半。
所以得到:
$$
r = \max_{\omega , b} 2 d \\
s.t. y_i \left( \frac{\omega^T}{||\omega||} + \frac{b}{||\omega||} \right) \ge d \qquad; for \quad i = 1, \dots,m
\tag{7}
$$
上式的意思是将$r$的条件约束在位于平面一侧的样本点。
引入一个新的概念,将间隔与法向量的长度结合在一起:
$$
\hat{d} = ||\omega||d
\tag{8}
$$
实际上,$\hat{d}$的取值,并不会影响最优化问题的解,这就使得我们在表达式中,引入任意值的$d$,一般我们将其定为1。
则:
$$
r = \max _ {\omega}\frac{2}{||\omega||} \\
s.t. y_i(\omega^Tx + b) \ge 1
\tag{9}
$$
上式为西瓜书中的$6.5$式,其等价于($\omega \ne 0$):
$$
r = \min _ {\omega} \frac{1}{2} ||\omega||^2 \\
s.t. y_i(\omega^T x_i + b) \ge 1 \quad ; i = 1,2,\dots, m
\tag{10}
$$
上式为西瓜书中的$6.6$式,起目的主要是为了将$(9)$式转化为凸形式。
SVM的性质
最大间隔超平面的存在具有唯一性
我们假设,现在具有两个最优解$(\omega^\star_1,b^\star_1)$和$(\omega^\star_2,b^\star_2)$,则:
- 证明:$\omega_1^* = \omega_2^*$(存在性证明):
根据假设,有$|| \omega_1^* || = || \omega_2^* || = c \ne 0 $,设$ \omega = \frac{ \omega_1^* + \omega_2^* }{2},b = \frac{
b_1^* + b_2^* }{2} $,则有:
$$
c \le ||\omega|| = \frac{|| \omega_1^\star + \omega_2^\star ||}{2} \le \frac{||\omega_1^\star ||+
||\omega_2^\star||}{2} = c \\
\Rightarrow ||\omega|| = \frac{|| \omega_1^\star + \omega_2^\star ||}{2} = \frac{||\omega_1^\star ||+
||\omega_2^\star||}{2} \\
\Rightarrow \underbrace{\omega_1^\star = k \omega_2^\star}_{Colinear} \\
\Rightarrow k =
\left \lbrace \begin{matrix} 1 \\ -1
\end{matrix}
\right . \Rightarrow \omega =
\left \lbrace \begin{align} \omega^\star_1 = \omega ^\star_2 \quad ;\ if \quad k = 1 .\\
0 \quad ;\ if \quad k = 1 .
\end{align}
\right . \Rightarrow \omega^\star_1 = \omega ^\star_2
\tag{11}
$$
$Colinear$是共线的意思,一个向量可以用另一个向量线性表示,则两个向量共线。
$k$只能取$+1,-1$的原因为$|| \omega_1^* || = || \omega_2^* ||$,两个向量共线且长度相等的话,要么真的相等,要么就是等长相反的两个向量,故$k$只能取$+1,-1$。
- 证明:$b_1^\star = b_2^\star$(唯一性证明)
设有四个点:$x_1^{‘},x_2^{‘} \in \lbrace x_i | y_i = +1 \rbrace,x_1^{‘’},x_2^{‘’} \in \lbrace x_i | y_i = -1
\rbrace$,即,在取得正负样本的部分中分别拿出两个样本,一共四个样本(两正两负)。且有:
$$
\left \lbrace
\begin{matrix}
\omega^T x_1^{‘} + b_1^\star = +1 \\
\omega^T x_2^{‘} + b_2^\star = +1 \\
\omega^T x_1^{‘’} + b_1^\star = -1 \\
\omega^T x_2^{‘’} + b_2^\star = -1 \\
\end{matrix}
\right .
$$
解得:
$$
\left \lbrace
\begin{matrix}
b_1^\star = -\frac{1}{2} \omega^T(x_1^{‘} + x_1^{‘’})\\
b_2^\star = -\frac{1}{2} \omega^T(x_2^{‘} + x_2^{‘’})
\end{matrix}
\right . \\
\Rightarrow b_1^\star - b_2^\star= - \frac{1}{2}
\left[ \omega^T(x_1^{‘} - x_2^{‘}) + \omega^T(x_1^{‘’} - x_2^{‘’}) \right]
$$
要证明$b_1^\star = b_2^\star$,则需要证明:
$$
\left \lbrace
\begin{matrix}
\omega^T x_2^{‘} + b_1^\star \ge 1 = \omega^T x_1^{‘} + b_1^\star \\
\omega^T x_1^{‘} + b_2^\star \ge 1 = \omega^T x_2^{‘} + b_2^\star \\
\omega^T x_2^{‘’} + b_1^\star \ge 1 = \omega^T x_1^{‘} + b_1^\star \\
\omega^T x_1^{‘’} + b_2^\star \ge 1 = \omega^T x_2^{‘’} + b_2^\star \\
\end{matrix}
\right . \Rightarrow \left \lbrace
\begin{matrix}
\omega^T (x_1^{‘} - x_2^{‘}) = 0 \\
\omega^T (x_1^{‘’} - x_2^{‘’}) = 0
\end{matrix}
\right .
\Rightarrow b_1^\star = b_2^\star
$$
证毕。

