人工神经网络中常见的一些激活函数
激活函数是什么?
神经元
人工神经元(Artificial Neuron),简称神经元(Neuron),是构成神经网络的基本单元,其主要是模拟生物神经元的结构和特性,接收一组输入信号并产生输出。
在 AI 领域,一个神经元的输入输出是这样的,接收$D$个输入$\lbrace x_1, x_2, \cdots, x_D
\rbrace$,令向量$𝒙 = [ x_1, x_2, \cdots, x_D]$来 表示这组输入,并用净输入(Net Input) $𝑧 ∈ ℝ$ 表示一个神经元所获得的输入信号$𝒙$的加权和:
$$
\begin{align}
z & = \sum_{d=1}^D \omega_d x_d + b \\
& = \omega^T x + b \tag{1}
\end{align}
$$
其中:$𝒘 = [𝑤_1, 𝑤_2, ⋯ , 𝑤_𝐷] ∈ ℝ^D$.
激活函数
然后让上述的$z$经过激活函数,就得到了我们的$\alpha$,具体如图:
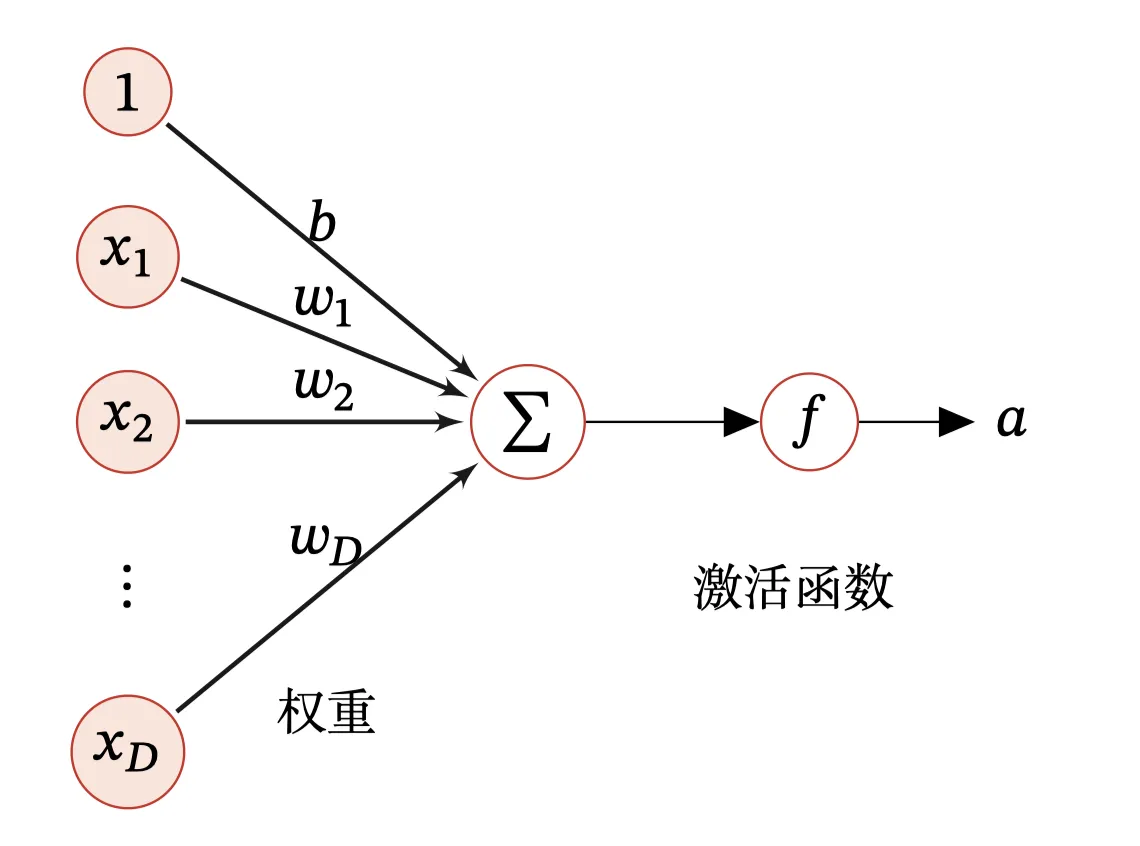
所以,激活函数其实是对神经元的处理结果的一个修饰,让其规范化,并且适应模型。
什么样的函数可以作为激活函数呢?需要满足这么几个条件:
- 连续并可导(允许少数点上不可导)的非线性函数.可导的激活函数可以直接利用数值优化的方法来学习网络参数.
- 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率.
- 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性.
常见的激活函数
函数的饱和性
对于函数 $𝑓(𝑥)$:
- 若 $𝑥 \rightarrow −\infty$ 时,其导数 $𝑓 ′ (𝑥) \rightarrow 0$,则称其为左饱和;
- 若 $𝑥 \rightarrow +\infty$ 时,其导数 $𝑓 ′ (𝑥) \rightarrow 0$,则称其为右饱和;
- 当同时满足左、右饱和时,就称为两端饱和.
激活函数的全家福
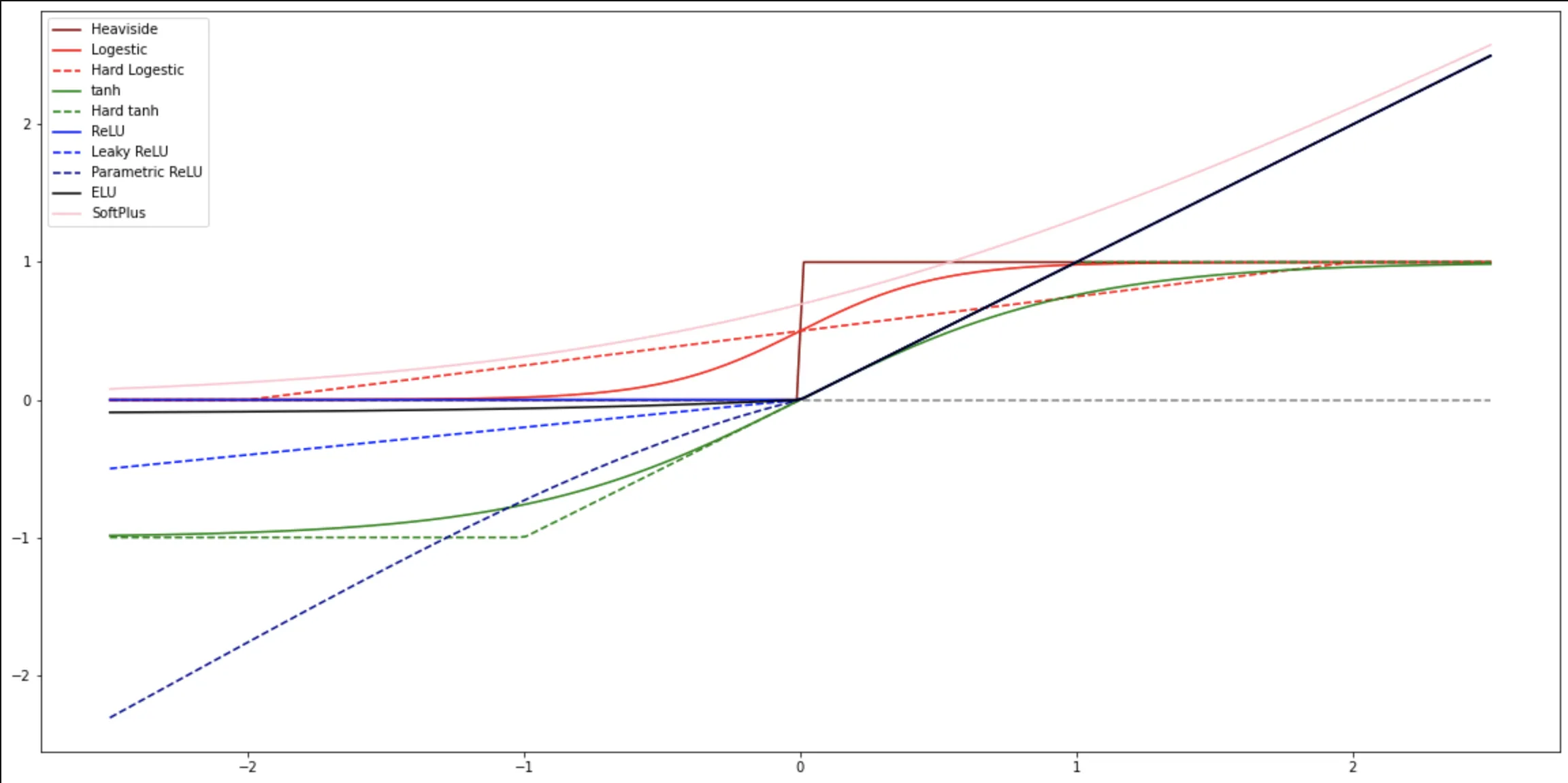
虽说是全家福,但是并没有将 Swish 函数、GeLU 函数、MaxOut 函数加到里面,如果加到里面的话,图就太复杂了,没法看了,下面会有单独的靓照。
By the way, 阶跃函数中间那点看着是不是好像是歪的? 没错,就是歪的(但是实际函数是直的哈,不要搞错了),我取 X 的离散点的时候,没有吧
0 取到里面,所以直接就从$f(0_-)$到了$f(0_+)$,有一个很小很小的偏差,不要在意这些细节。
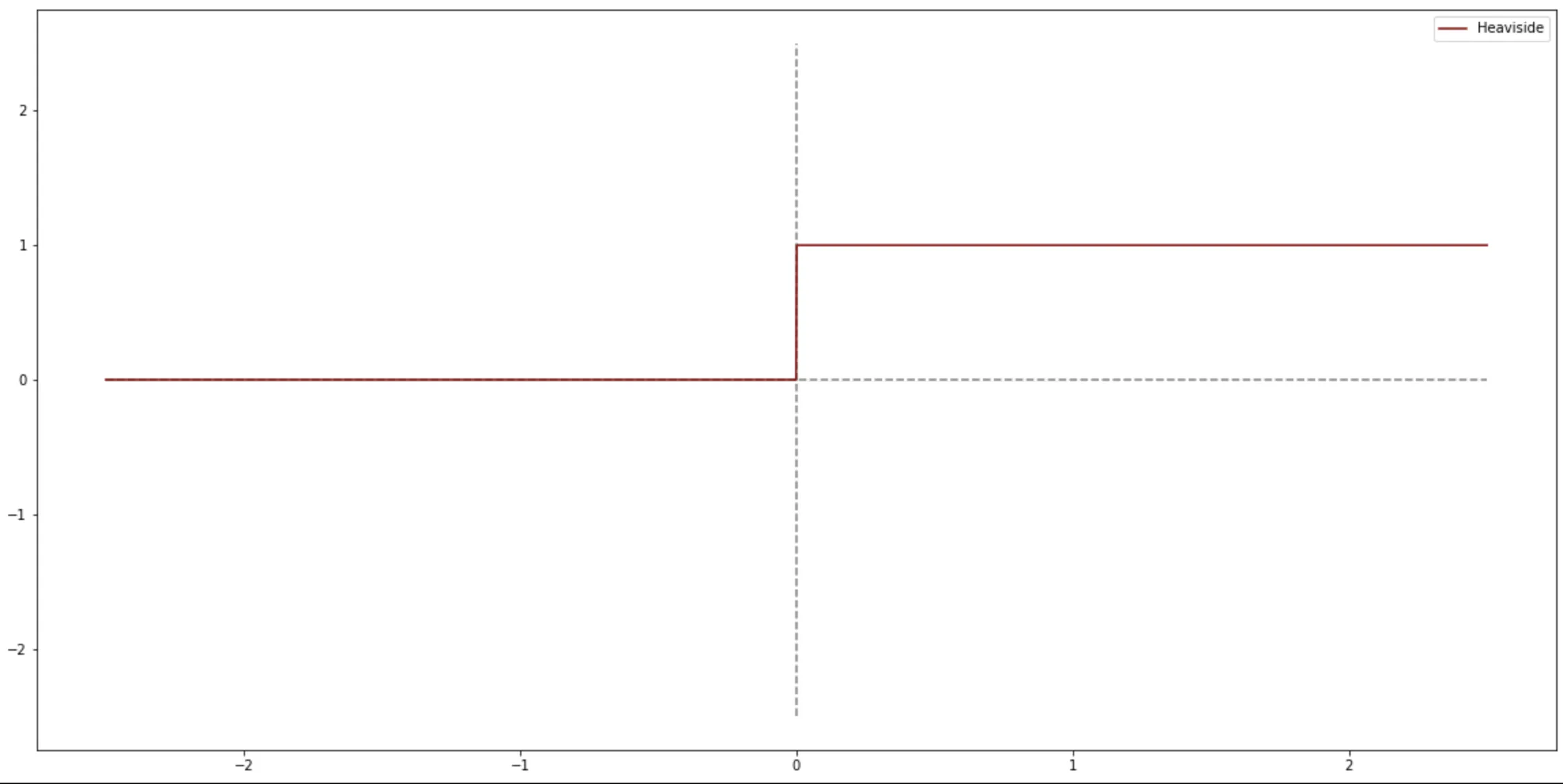
阶跃函数(Heaviside 函数)
$$
Heaviside(x) = \left \lbrace \begin{align} 1,& \qquad x \ge 0 \\ 0,& \qquad x < 0 \end{align} \right . \tag{2}
$$
简单粗暴,给人的感觉很容易计算,其实呢,给计算机也很容易计算,但是有一个问题,就是我们的机器学习,尤其是深度学习,在很大程度上是在求解一个最优化问题,在这样的前提下,我们再去看阶跃函数,就会发现,这个函数虽然很好算,但是不可微,没法求导在凸优化中就不好计算最优了。
1 | X = np.linspace(-2.5,2.5,2000) # X 为图像的定义域 |
Logestic 函数
Logestic 函数和 tanh 函数都是 Sigmoid 型函数,Sigmoid 的本意也就是
S型的意思,如果看他们的图像,你很容易就明白了。
$$
Logestic(x) = \frac{1}{1+e^{-x}} \tag{3.1}
$$
Logistic 函数可以看成是一个“挤压”函数,把一个实数域的输入“挤压”到$ (0, 1)$.当输入值在 $0$ 附近时,$Sigmoid$
型函数近似为线性函数;当输入值靠近两端时,对输入进行抑制.输入越小,越接近于 $0$ ;输入越大,越接近于
$1$.这样的特点也和生物神经元类似,对一些输入会产生兴奋(输出为 $1$ ),对另一些输入产生抑制(输出为 $0$
).和感知器使用的阶跃激活函数相比,Logistic 函数是连续可导的,其数学性质更好(相比阶跃函数来说).
因为 Logistic函数的性质,使得装备了 Logistic 激活函数的神经元具有以下两点性质:
- 其输出直接可以看作概率分布,使得神经网络可以更好地和统计学习模型进行结合.
- 其可以看作一个软性门(
Soft Gate),用来控制其他神经元输出信息的数量.
Logestic 函数的一个奇特的性质
$$
Logestic ‘(x) = Logestic(x) [1- Logestic(x)] \tag{3.2}
$$
所以说,Logestic 函数的导数比较好计算。
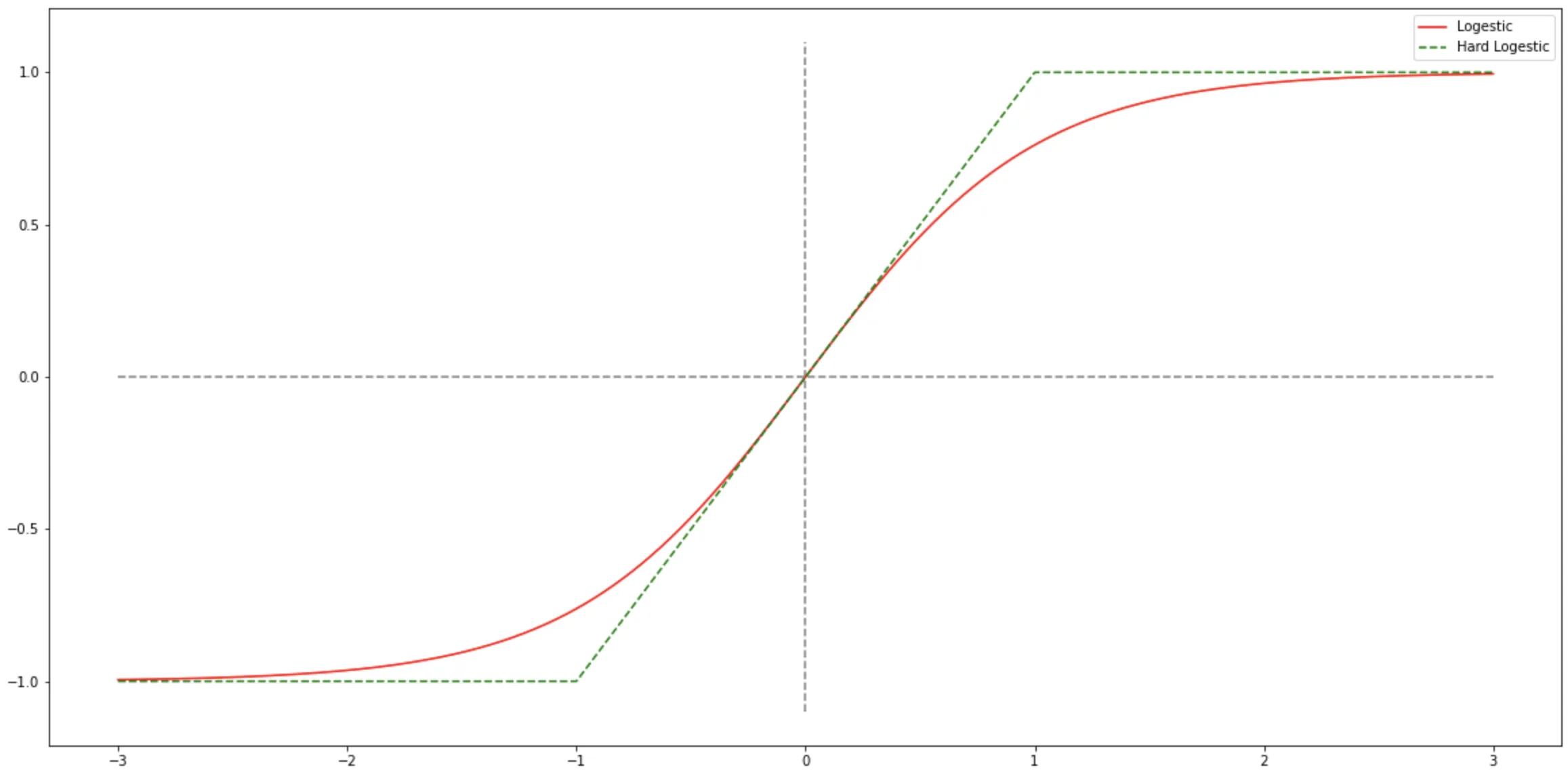
Hard-Logestic 函数
虽然说,Logestic 函数的导数比较好计算,但是,毕竟其中还是有一些求解$e$的指数值的操作,这样对于很大的模型来说,计算量增加的不是一点。所以,我们可以偷个懒,
寻找一种代替的解决办法。
所谓Hard-Logestic函数就是通过泰勒公式,在$0$点展开 Logestic 函数(即麦克劳林展开),只取前两项或者前 n 项来解决这个问题。
$$
\begin{align}
g_l(x) & ≈ 𝜎(x) + x \times 𝜎 ‘ (x) \\
& = 0.25𝑥 + 0.5
\end{align} \tag{3.3}
$$
$$
\begin{aligned}
HardLogestic(x) & = \left \lbrace
\begin{align}
1 & \qquad g_l(x) \ge 1 ; \\
g_l & \qquad 0 \lt g_l(x) \le 1 ; \\
0 & \qquad g_l(x) \le 0
\end{align}
\right . \\
& = \max ( \min(g_l(x), 1), 0) \\
& = \max ( \min(0.25x + 0.5, 1), 0)
\end{aligned} \tag{3.4}
$$
这样,就可以把指数运算转换成了加减乘除和比大小了。
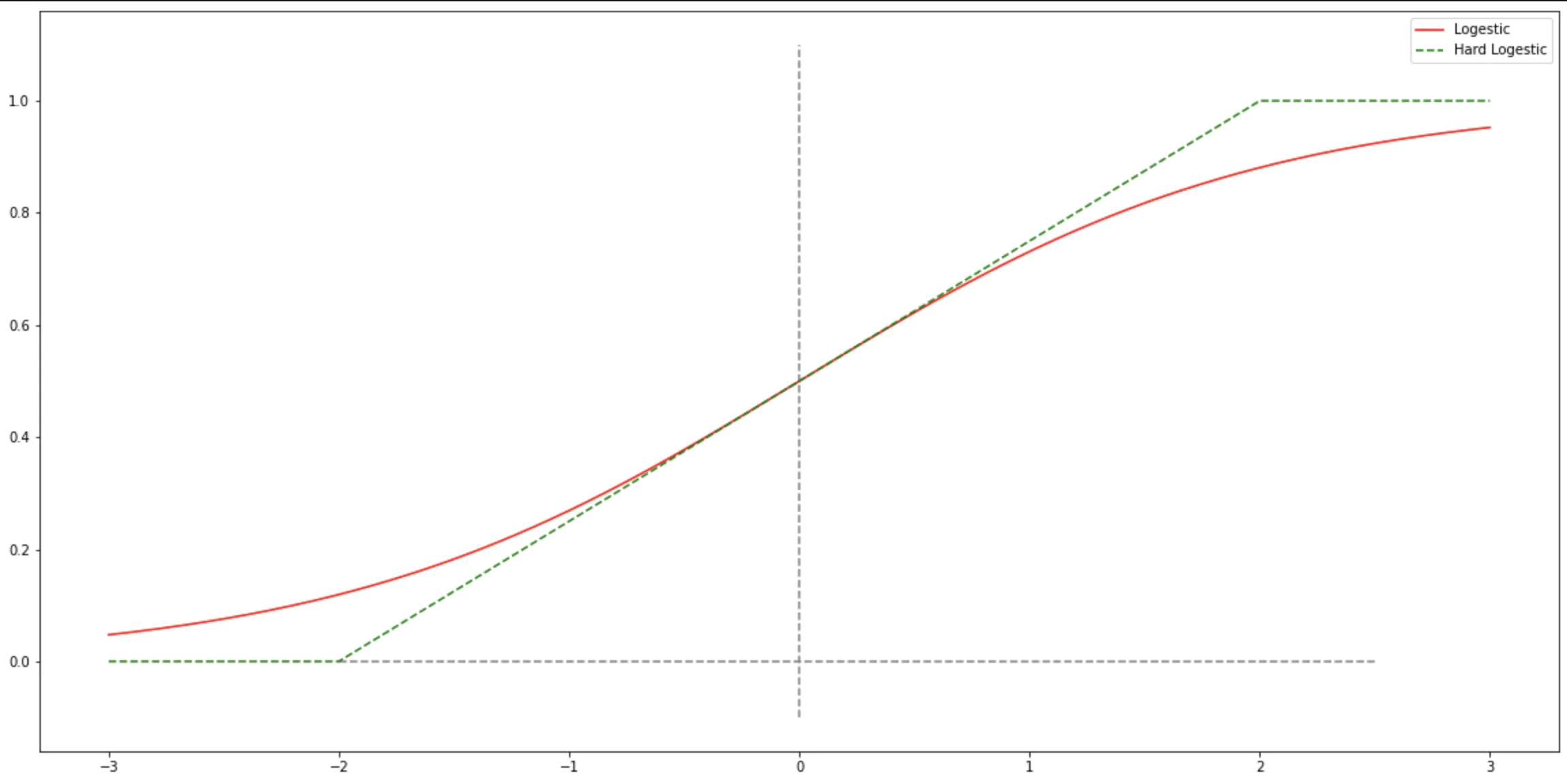
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
tanh 函数
$$
tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \tag{4.1}
$$
Tanh 函数可以看作放大并平移的 Logistic函数,其值域是$(−1, 1)$.
tanh 函数的输出是零中心化的(Zero-Centered),而 Logistic 函数的输出恒大于 0.
非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(Bias Shift),并进一步使得梯度下降的收敛速度变慢.
Hard-tanh 函数
同样因为其计算的难度,我们可以使用泰勒展开式(麦克劳林展开)来近似的逼近tanh函数。
$$
\begin{align}
g_t(x) & ≈ \tanh(0) + x \times \tanh ‘ (0) \\
& = x
\end{align} \tag{4,2}
$$
$$
\begin{align}
hard\tanh(𝑥) = \max ( \min(g_t(x), 1), −1) \\ = \max ( \min(𝑥, 1), −1)
\end{align} \tag{4.3}
$$
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
非零中心化的输出会 使得其后一层的神经元的输入发生偏置偏移(Bias Shift),并进一步使得梯度下 降的收敛速度变慢.
ReLU 函数
$ReLU$(Rectified Linear Unit,修正线性单元),也叫 Rectifier 函数,是目前深度神经网络中经常使用的激活函数. $ReLU$
实际上是一个斜坡(ramp)函数,定义为:
$$
ReLU = \left \lbrace
\begin{align}
x & \qquad x \gt 0; \\
0 & \qquad x \le 0
\end{align}
\right .
\tag{5.1}
$$
我们可以发现,其实 $ReLU$ 函数就是一个高通滤波器,他过滤掉了所有小于 $0$ 的值,对于所有大于 $0$ 的值则原样输出。
优点
采用 $ReLU$ 的神经元只需要进行加、乘和比较的操作,计算上更加高效.Sigmoid 型激活函数会导致一个非稀疏的神经网络,而 $ReLU$
却具有很好的稀疏性,大约 50% 的神经元会处于激活状态.
在优化方面,相比于 Sigmoid型函数的两端饱和,ReLU 函数为左饱和函数, 且在 𝑥 > 0 时导数为
1,在一定程度上缓解了神经网络的梯度消失问题,加速梯度下降的收敛速度.
缺点
$ReLU$ 函数的输出是非零中心化的,给后一层的神经网络引入偏置偏移, 会影响梯度下降的效率.此外,ReLU 神经元在训练时比较容易“死亡”.在训
练时,如果参数在一次不恰当的更新后,第一个隐藏层中的某个 ReLU 神经元在 所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是
0,在以后的训练过程中永远不能被激活(在上一层神经网络中已经被滤掉了,所以以后就不会再有了,
问题在于你根本不知道以后会不会用到这些神经元中的信息).这种现象称为死亡 $ReLU$ 问题(Dying ReLU Problem),并且也有可能会发生在其他隐藏层.
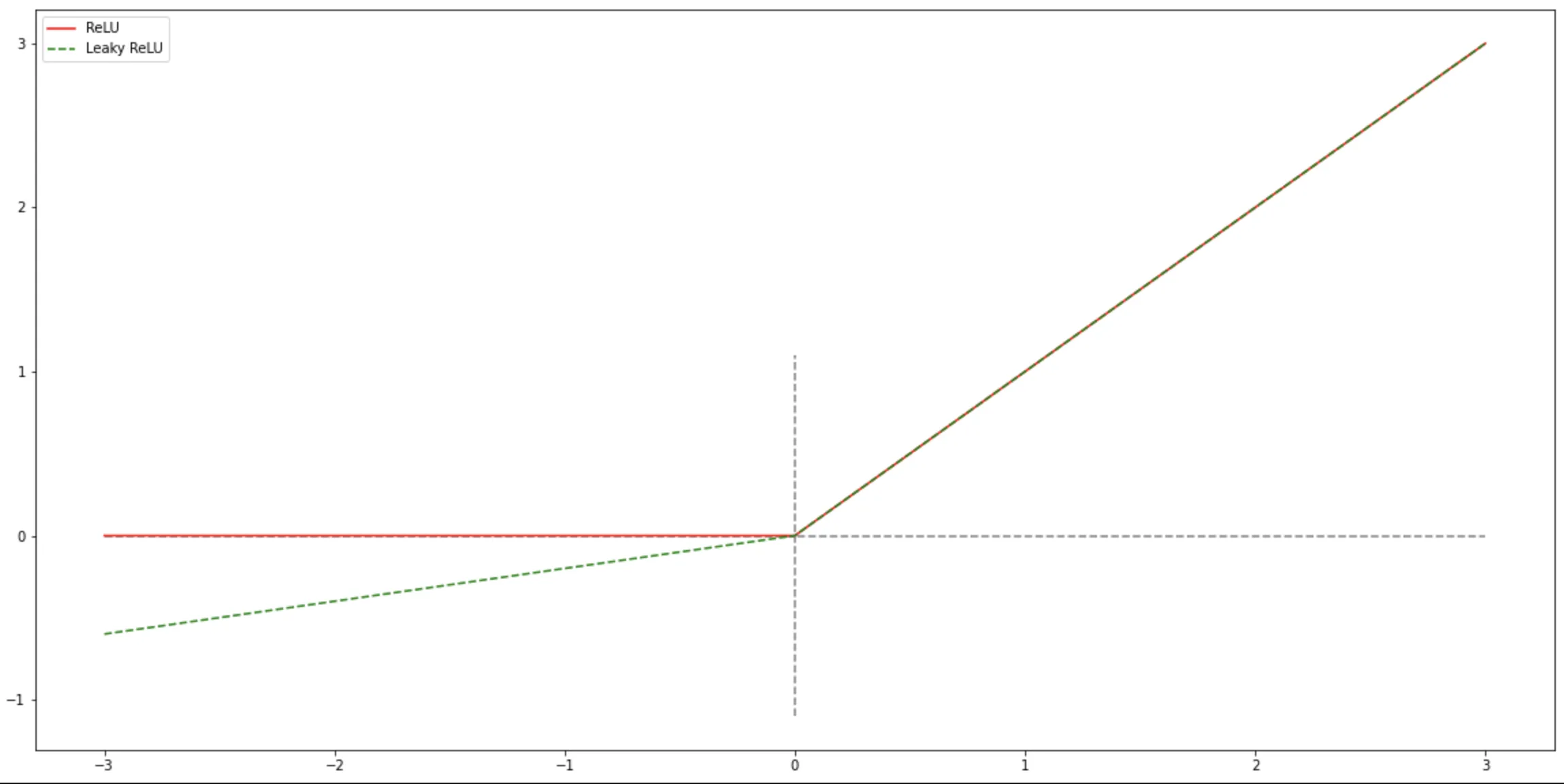
Leaky ReLU
为了防止神经元私网的问题,我们引入了 LeakyRelu 函数,这个函数的主要目的是,在 x 小于 0
的时候,给他一个很小的系数,让该神经元的影响尽可能的小,而不是直接将他过滤掉。
$$
\begin{aligned}
LeakyReLU(𝑥) & = \left \lbrace
\begin{align}
x &\qquad x \gt 0; \\
\gamma x & \qquad x \le 0
\end{align}
\right . \\
& = \max(x, \gamma x),
\end{aligned}
\tag{5.2}
$$
Parametric ReLU
带参数的 ReLU(Parametric ReLU,PReLU)引入一个可学习的参数,不同神经元可以有不同的参数.对于第 i 个神经元,其 PReLU 的
定义为:
$$
\begin{aligned}
ParametricReLU(𝑥) & = \left \lbrace
\begin{align}
x &\qquad x \gt 0; \\
\gamma_i x & \qquad x \le 0
\end{align}
\right . \\
& = \max(x, \gamma_i x),
\end{aligned}
\tag{5.3}
$$
如果$ 𝛾_𝑖= 0$,那么 PReLU 就退化为 ReLU.如果$ 𝛾_𝑖 $为一个很小的常数,则 PReLU 可以看作带泄露的 ReLU.PReLU
可以允许不同神经元具有不同的参数,也可以一组神经元共享一 个参数.
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
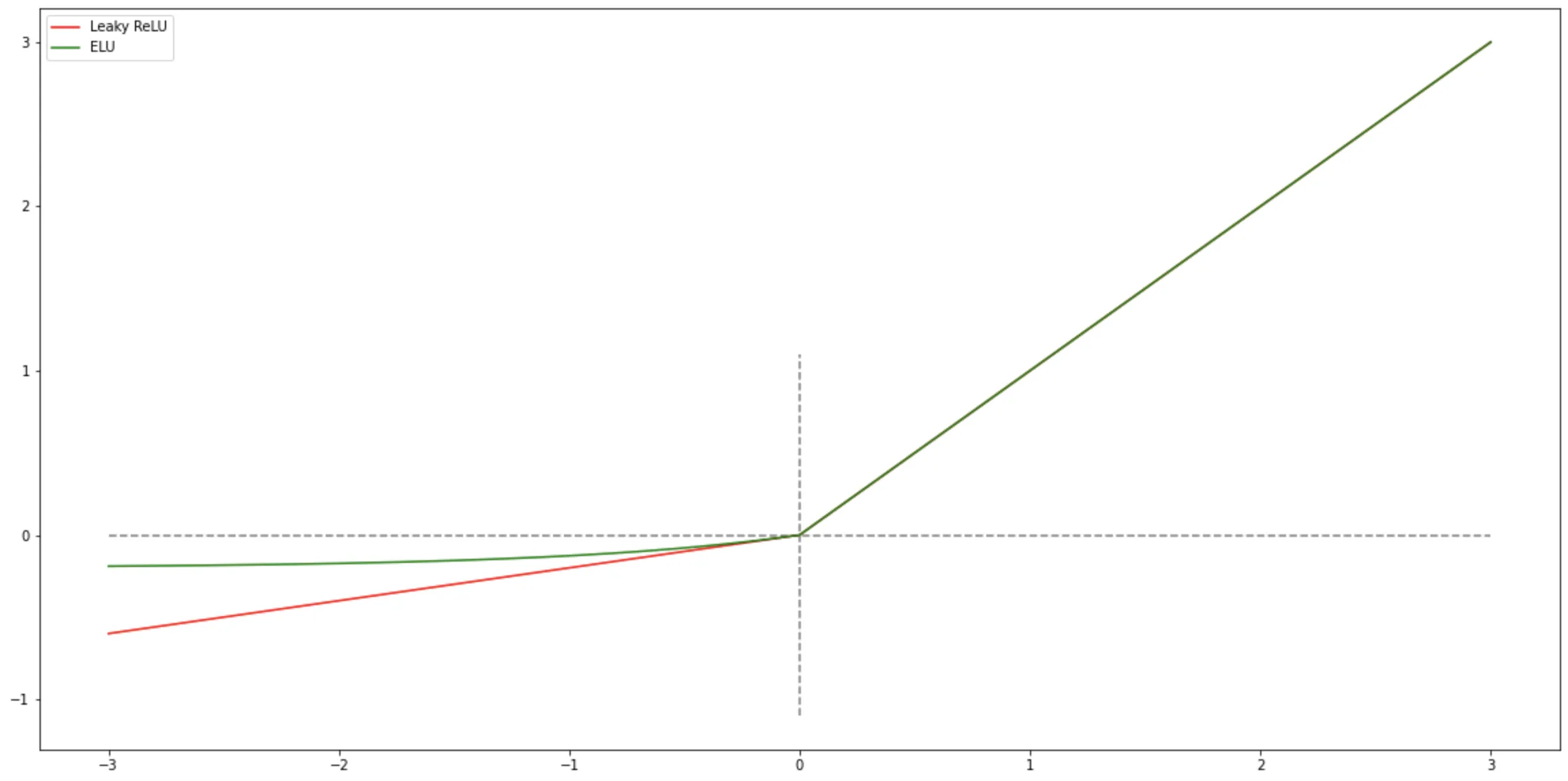
ELU 函数
ELU(Exponential Linear Unit,指数线性单元)[Clevert et al., 2015] 是一个近似的零中心化的非线性函数,其定义为
$$
\begin{aligned}
ELU(𝑥) & = \left \lbrace
\begin{align}
x &\qquad x \gt 0; \\
\gamma_i (e^x - 1) & \qquad x \le 0
\end{align}
\right . \\
& = \max(x, \gamma_i (e^x - 1)),
\end{aligned}
\tag{6}
$$
其中$ 𝛾 ≥ 0$ 是一个超参数,决定 $𝑥 ≤ 0 $时的饱和曲线,并调整输出均值在$ 0$ 附近.
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
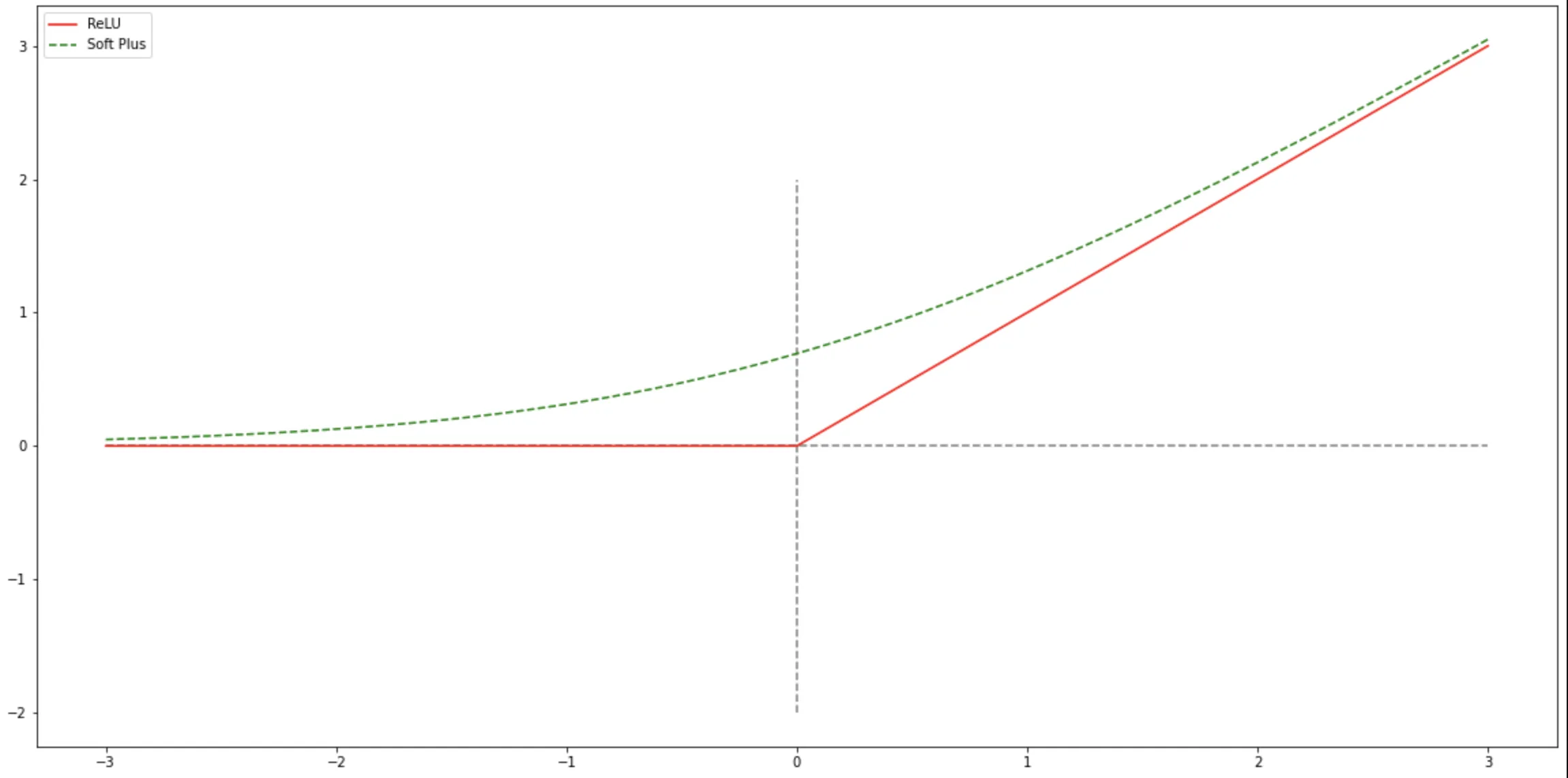
SoftPlus 函数
Softplus 函数可以看作 Rectifier 函数(ReLU函数)的平滑版本,其定义为:
$$
Softplus(𝑥) = \log(1 + e^x) \tag{7}
$$
Softplus函数其导数刚好是 Logistic 函数.Softplus 函数虽然也具有单侧抑制、宽兴奋边界的特性,却没有稀疏激活性.
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
Swish 函数
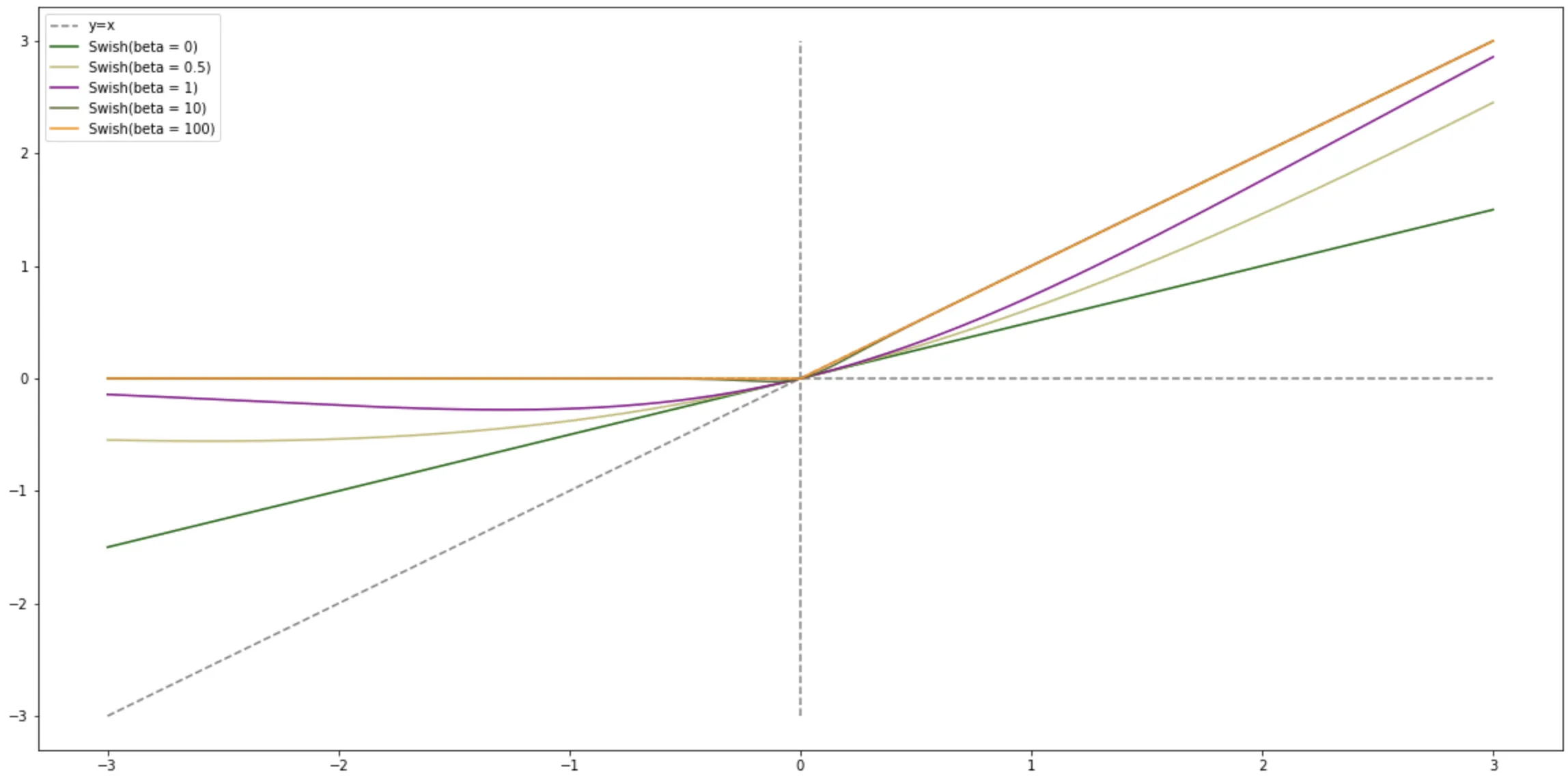
Swish 函数是一种自门控(Self-Gated)激活函数,定义为:
$$
swish(x) = x 𝜎 (\beta x) \tag{8}
$$
其中$𝜎(⋅)$ 为 Logistic 函数,$𝛽$ 为可学习的参数或一个固定超参数.$𝜎(⋅) ∈ (0, 1)$ 可 以看作一种软性的门控机制.当 $𝜎(𝛽𝑥)$
接近于 1 时,门处于“开”状态,激活函数的输出近似于 $𝑥$ 本身;当$ 𝜎(𝛽𝑥)$ 接近于 0 时,门的状态为“关”,激活函数的输出近似于 $0$.
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
当$ 𝛽 = 0 $时,Swish 函数变成线性函数 $\frac{x}{2}$ .当 $𝛽 = 1$ 时,Swish 函数在 $𝑥 > 0$ 时近似线性,在 $𝑥 < 0$
时近似饱和,同时具有一定的非单调性.当 $𝛽 → +∞\infty$ 时,$𝜎(𝛽𝑥)$ 趋向于离散的 $0-1$ 函数,Swish 函数近似为 ReLU
函数.因此,Swish 函数可以看作线性函数和 ReLU 函数之间的非线性插值函数,其程度由参数 𝛽 控制.
GELU 函数
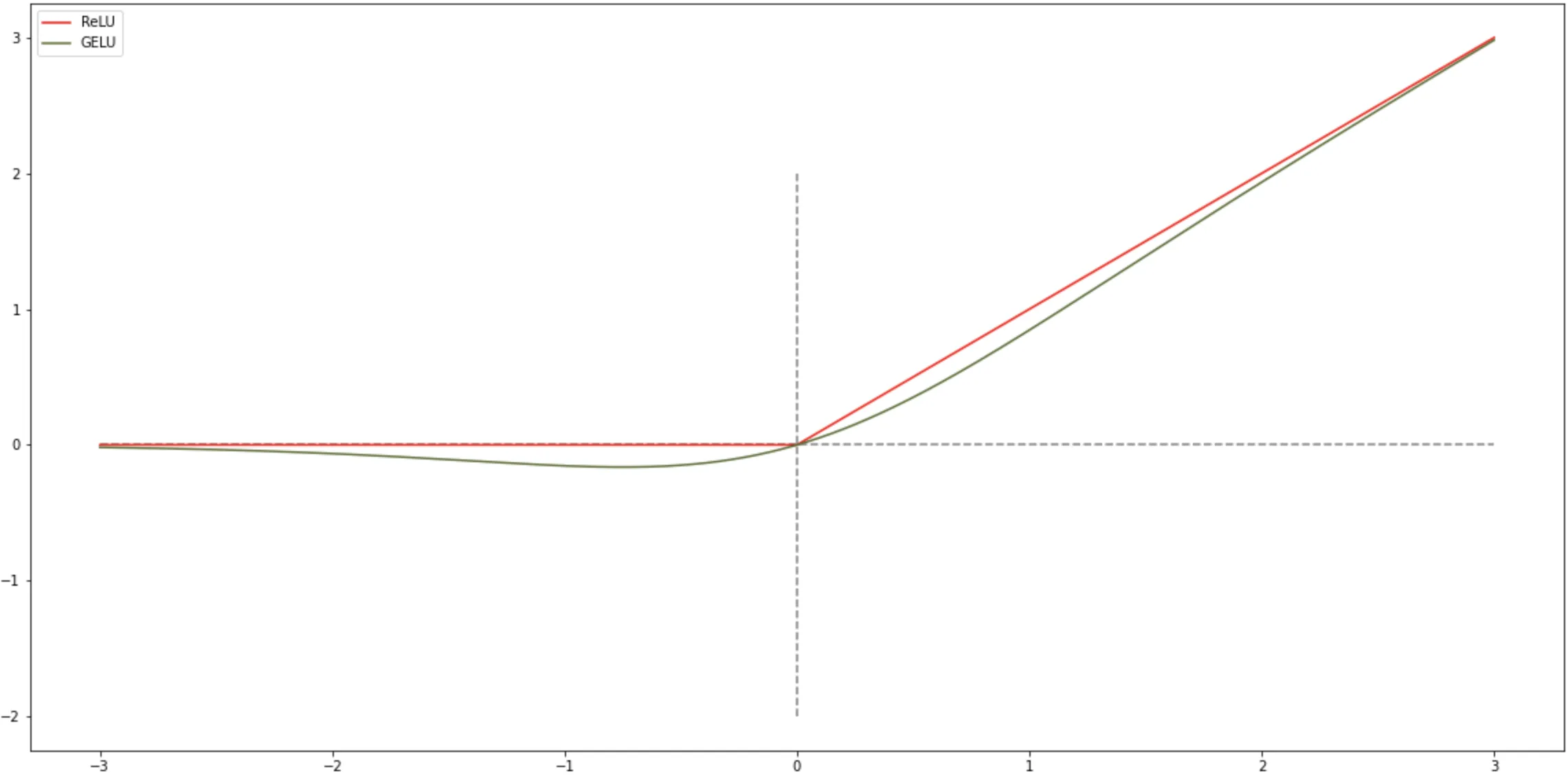
GELU(Gaussian Error Linear Unit,高斯误差线性单元)也是一种通过门控机制来调整其输出值的激活函数,和 Swish 函数比较 类似.
$$
GELU(𝑥) = 𝑥𝑃(𝑋 ≤ 𝑥) \tag{9.1}
$$
其中 $𝑃(𝑋 ≤ 𝑥)$ 是高斯分布 $𝒩(𝜇, 𝜎^2 )$ 的累积分布函数,其中 $𝜇, 𝜎$ 为超参数,一般设 $𝜇 = 0, 𝜎 = 1$ 即可.由于高斯分布的累积分布函数为
S 型函数,因此 GELU 函数可以用 Tanh 函数或 Logistic 函数来近似,
$$
GELU(𝑥) ≈ 0.5𝑥 \left ( 1 + \tanh \left ( \sqrt{\frac{2}{\pi}} \left ( x + 0.044715 x ^ 3 \right ) \right ) \right )
\tag{9.2}
$$
或
$$
GELU(𝑥) ≈ 𝑥𝜎(1.702𝑥) \tag{9.3}
$$
当使用 Logistic 函数来近似时,GELU 相当于一种特殊的 Swish 函数.
1 | X = np.linspace(-3,3,2000) # X 为图像的定义域 |
人工神经网络中常见的一些激活函数

