感知机模型
感知机模型( Perceptron Learning Algorithm )的基础属性
| 属性 | 属性值 |
|---|---|
| 输入空间 | $X \subseteq R_n$ |
| 输入变量 | $x \in X$ |
| 输出空间 | $Y = { +1, -1}$ |
| 输出变量 | $y \in { +1, -1}$ |
| 假设空间 | $\mathcal{H}=\lbrace f | f(x)=sign(\omega\cdot x+b)\rbrace$ |
模型适用条件
感知机模型的适用条件是数据集需要线性可分,具体线性可分的概念如下:
给定一个数据集
$$
\mathcal{D} = { (x_1,y_1), (x_2,y_2), \cdots , (x_n,y_n) }
$$其中,$x_i \in \mathcal{X} = R^n, y_i \in \mathcal{Y} = {+1, -1}, i = 1,2,\cdots, n$。如果存在某个超平面$S$:
$$
w \cdot x + b = 0
$$能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即:对所有$y_i=+1$的实例$i$,有 $ω \cdot x_i + b \gt
0$,对所有$y_i=−1$的实例$i$,有$ω \cdot x_i+ b \lt 0$,则数据集$\mathcal{D}$为线性可分数据集$(linearly\ separable\ data
set)$;否则,称数据$\mathcal{D}$集线性不可分。
可视化表示
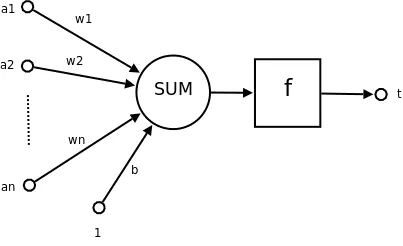
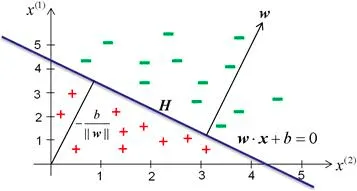
感知机模型的学习策略
损失函数
误分类点到超平面的总距离:
$$
L(w, b) = - \sum_{x_i \in M} y_i (w \cdot x_i + b)
\tag{1}
$$
- 其中,$y_i$表示第$i$个点的分类是否正确, 因为 $y_i$ 和 $w \cdot x_i + b$都是带符号的, 所以当二者不一致(即为分类错误)
的时候,就会导致其乘积为负,故需要在前面加上负号.- 其中, $M$ 为所有误分类点的集合.
感知机模型的输入和输出
总结一下目前用到的符号,我们需要知道以下数学符号的含义:
| 负号 | 含义 |
|---|---|
| $\mathcal{H}$ | 假设空间 |
| $f(x) \in \mathcal{H}$ | 感知机模型 |
| $\chi \subseteq R^n$ | 特征空间 |
| $\mathcal{Y} = { +1, -1}$ | 输出空间 |
| $R^n$ | $n$ 维向量空间 |
| $w = [w^{(1)},w^{(2)},w^{(3)},\cdots, w^{(n)}]$ | 超平面的法向量,或者说特征的参数向量 |
| $w^{(i)}, (i = 1,2,3,\cdots,n)$ | 超平面的法向量的分量,或者说某个参数 |
| $x = [x^{(1)},x^{(2)},x^{(3)},\cdots, x^{(n)}]$ | 输入向量,特征向量 |
| $x^{(i)}, (i = 1,2,3,\cdots,n)$ | 特征向量中的某个特征 |
| $b$ | 超平面的截距 |
| $sign(x)$ | 符号函数,$x \ge 0$时为 $+1$,否则为$-1$ |
| $\mathcal{D} = (x_1,y_1), (x_2,y_2), \cdots ,(x_m,y_m)$ | 数据集, $m$ 为样本数, $n$ 为特征数,$y$ 为分类标签($1$或者$-1$) |
感知机模型学习算法
感知机模型学习算法的原始形式
随机梯度下降法
给定一个训练集
$$
\mathcal{T} = { (x_1,y_1), (x_2,y_2), \cdots , (x_N,y_N) }
$$
其中,$x_i \in \mathcal{X} = R^n, y_i \in \mathcal{Y} = {+1, -1}, i = 1,2,\cdots, N$,求参数$w,b$使其为以下损失函数极小化问题的解:
$$
\min_{w,b} L(w,b) = - \sum_{x_i \in M} y_i (w \cdot x_i + b) \tag{2}
$$
对于上述函数,我们分别对$w,b$求梯度:
$$
\left \lbrace
\begin{aligned}
\frac{\partial L (w,b)}{\partial w} & = \nabla_w L(w,b) = - \sum_{x_i \in M} y_i x_i \\
\frac{\partial L (w,b)}{\partial b} & = \nabla_b L(w,b) = - \sum_{x_i \in M} y_i
\end{aligned}
\right .
\tag{3}
$$
故,PLA 的迭代公式为:
$$
\left \lbrace
\begin{matrix}
w \leftarrow & w + \eta y_i x_i \\
b \leftarrow & b + \eta y_i
\end{matrix}
\right .
\tag{4}
$$
此处如果按照正常的梯度下降算法的话,每一个$w$更新的时候,所减去的梯度均为每一个节点计算的梯度.但是,在随机梯度下降算法中,尤其是本例中,会选择当前所迭代的节点所计算出的梯度来进行迭代(
下降).即为随机梯度下降的一种.
算法:
输入: 训练数据集$\mathcal{T}$; 学习率$\eta (0 \lt \eta \le 1)$.
输出: $w,b$, 以及感知机模型$f(x)= sign(w \cdot x + b)$.
迭代过程:
选取初始值$w_0, b_0$, 一般取$(w,b) = (1,0)\ or\ (0,0)$
在训练集$\mathcal{T}$中选取数据$(x_i, y_i)$;
如果$y_i (w \cdot x_i + b) \le 0$, 即表示该节点预测错误;
该处的等于号是表示,当前节点刚好在分割超平面上, 也是属于没有分类成功的情况,所以需要重新调整分割超平面,即$w,b$
$$
\left \lbrace
\begin{matrix}
w \leftarrow & w + \eta y_i x_i \\
b \leftarrow & b + \eta y_i
\end{matrix}
\right .
\tag{4}
$$
- 转到$2$, 直至训练集中没有错误分类点.
感知机模型的对偶形式
PLA 对偶形式的基本思想是,将公式$(4)$改写为实例$x_i$和标记$y_i$的线性组合,具体如下:
我们假设当前为第$n$次迭代,则下一次的迭代为:
$$
\left \lbrace
\begin{aligned}
w_{n+1} & = w_n + \eta y_i x_i \\
b_{n+1} & = b_n + \eta y_i
\end{aligned}
\right .
\tag{4.1}
$$
则可以根据地推公式,得到:
$$
\left \lbrace
\begin{aligned}
w_{n+1} = & \quad w_n + \eta y_i x_i = w_{n-1} + \eta y_i x_i + \eta y_{i-1} x_{i-1} = \cdots \\
b_{n+1} = & \quad b_n + \eta y_i = b_{n-1} + \eta y_i + \eta y_{i-1} = \cdots
\end{aligned}
\right .
\tag{4.2}
$$
所以,我们可以将$w,b$写成:
$$
\left \lbrace
\begin{aligned}
w & = \sum_{i=1}^N \alpha_i y_i x_i \\
b &= \sum_{i=1}^N \alpha_i y_i
\end{aligned}
\right .
\tag{5}
$$
这里我们对比$5$和$4.2$,其中的$\alpha_i = n_i \eta,(\alpha_i \ge 0, i=1,2,\cdots,N)$,
表示第$i$个实例点由于误分而进行更新的次数,这样的话,意味着它距离分割超平面越近, 也就越难正确分类. 这样的实例点对于学习结果的影响最大.
算法
输入: 线性可分的数据集$\mathcal{T} = \lbrace (x_1, y_1), (x_2, y_2), \cdots, (x_N, y_n) \rbrace$, 其中$x_i \in R^n, y_i
\in \lbrace -1, +1 \rbrace, i = 1,2,\cdots, N$; 学习率$\eta ( 0 \lt \eta \le 1)$.
输出: $\alpha, b$; 感知机模型 $f(x) = sign\left ( \sum_{j=1}^N \alpha_j y_j x_j \cdot x + b \right )$; 其中 $\alpha = (
\alpha_1, \alpha_2, \cdots, \alpha_N)^T$.
- $\alpha \leftarrow 0, b \leftarrow 0$;
- 在训练集中选择数据$(x_i,y_i)$;
- 如果$y_i \left ( \sum_{j=1}^N \alpha_j y_j x_j \cdot x + b \right ) \le 0$,
$$
\left \lbrace
\begin{aligned}
\alpha_i \leftarrow \alpha_i + \eta \\
b \leftarrow b + \eta y_i
\end{aligned}
\right .
\tag{4.2}
$$
- 转至$(2)$直至没有误分类数据.
PLA 算法的收敛性
设存在一个超平面$\mathcal{S}$, 可以完全正确划分数据集$\mathcal{D}$, 其法向量为$\hat{w}_{opt}$.
令$\gamma = \min_{0 \le i \le m} y_i (\hat{w}_{opt} \cdot x)
$,即$\gamma$为离超平面最近的数据点与超平面的距离,$m$为样本数量。那么,对于任意的点$\hat{x}_i$均有:
$$
y_i(\hat{w} \cdot \hat{x}_i ) \ge \gamma \tag{6}
$$
所有样本距离分割超平面的距离均大于最小距离(显然)。
令感知机算法从$\hat{w}_0 = 0$开始,每遇到错误分类就更新参数向量,令$\hat{w}_
{k-1}$为遇到第$k$个错误分类之前的参数向量,则遇到第$k$个误分类情况时需要满足:
$$
y_i (\hat{w}_{k-1} \cdot \hat{x}_i) \le 0 \tag{7}
$$
第$k$个样本点是分类错误的。
若$(\hat{x}_i, y_i)$是被$\hat{w}_{k-1}$错误分类的数据,则更新参数向量:
$$
\hat{w}_k = \hat{w}_{k-1} + y_i \hat{x}_i \tag{8}
$$
因为:
$$
\hat{w}_k \cdot \hat{w}_{opt} \ge k \gamma \tag{9}
$$
$$
\Vert \hat{w}_k\Vert ^2 \le k R^2 \tag{10}
$$
故:
$$
1 \ge cos\theta = \frac{\hat{w}_k \cdot \hat{w}_{opt}}{\Vert \hat{w}_k\Vert \cdot\Vert \hat{w}_{opt}\Vert } \ge
\frac{k \gamma}{\Vert \hat{w}_k\Vert \cdot\Vert \hat{w}_{opt}\Vert } \ge \frac{k \gamma}{\sqrt{kR^2} \Vert
\hat{w}_{opt}\Vert } \tag{11}
$$
其中,$\theta$为$\hat{w}_k$和$\hat{w}_{opt}$的夹角。
所以由上面的不等式可以得知:
$$
k \le \frac{R^2\Vert \hat{w}_{opt}\Vert ^2}{\gamma^2} \tag{12}
$$
所以,感知机的错误修正次数是有上限的,由于$\Vert \hat{w}_{opt}\Vert $是必然存在的,所以$k$一定存在。即感知机算法是收敛的。
注
注 1: 式$(9)$证明
$$
\hat{w}_k \cdot \hat{w}_{opt} \ge k \gamma \tag{9}
$$
$$
\begin{aligned}
\hat{w}_k \cdot \hat{w}_{opt} & = \hat{w}_{k-1} \cdot \hat{w}_{opt} + y_i \hat{x}_i \hat{w}_{opt} \\
& \ge \hat{w}_{k-1} \cdot \hat{w}_{opt} + \gamma
\end{aligned}
\tag{9.1}
$$依次递推:
$$
\begin{aligned}
\hat{w}_{k-1} \cdot \hat{w}_{opt} & = \hat{w}_{k-2} \cdot \hat{w}_{opt} + y_i \hat{x}_i \hat{w}_{opt} \\
& \ge \hat{w}_{k-2} \cdot \hat{w}_{opt} + \gamma
\end{aligned}
\tag{9.2}
$$故得到递推式:
$$
\begin{aligned}
\hat{w}_k \cdot \hat{w}_{opt} & = \hat{w}_{k-1} \cdot \hat{w}_{opt} + y_i \hat{x}_i \hat{w}_{opt}
\\ & \ge \hat{w}_{k-1} \cdot \hat{w}_{opt} + \gamma
\\ & = \hat{w}_{k-2} \cdot \hat{w}_{opt} + y_i \hat{x}_i \hat{w}_{opt} + \gamma
\\ & \ge \hat{w}_{k-2} \cdot \hat{w}_{opt} + 2\gamma
\\ & \cdots
\\ & \ge \hat{w}_0 \cdot \hat{w}_{opt} + k \gamma
\\ &= k \gamma
\end{aligned}
\tag{9.1}
$$
注 1:式$(10)$证明
$$
\Vert \hat{w}_k\Vert ^2 \le k R^2 \tag{10}
$$
$$
\Vert \hat{w}_k \Vert ^ 2 = \Vert \hat{w}_{k-1} \Vert ^2 + 2 y_i \cdot \hat{w}_{k-1} \cdot \hat{x}_i + y_i^2 \cdot
\Vert \hat{x}_i \Vert ^2 \\
y_i \in \lbrace +1 , -1 \rbrace \rightarrow 省略y_i^2
$$因为所有需要处理的数据点都是错误分类,故:
$$
y_i \cdot \hat{w}_{k-1} \cdot \hat{x}_i \le 0
$$
所以:
$$
\Vert \hat{w}_k \Vert ^2 \le \Vert \hat{w}_{k-1} \Vert ^2 + \Vert \hat{x}_i \Vert ^2
$$
令$R = \max_{0 \le i \le m} \Vert \hat{x}_i \Vert$,即,离原点最远的点与原点的距离。则:
$$
\Vert \hat{w}_{k} \Vert^2 \le \Vert \hat{w}_{k-1} \Vert^2 + R^2
$$
依次递推:
$$
\Vert \hat{w}_{k-1} \Vert^2 \le \Vert \hat{w}_{k-2} \Vert^2 + R^2
$$
故:
$$
\begin{aligned}
\Vert \hat{w}_{k} \Vert ^2 & \le \hat{w}_{k-1} + R^2 \\
& \le \hat{w}_{k-2} + 2 R^2 \\
& \cdots \\
& \le \hat{w}_{1} + (k-1)R^2 \\
& \le \hat{w}_{0} + k\cdot R^2 \\
& = k\cdot R^2 \\
\end{aligned}
$$

