深度学习的数学知识-微积分相关概念
本文主要记录我在学习机器学习过程中对梯度概念复习的笔记,主要参考《高等数学》《简明微积分》以及维基百科上的资料为主,文章小节安排如下:
1)导数 2)导数和偏导数 3)导数与方向导数 4)导数与梯度 5)梯度下降法
导数
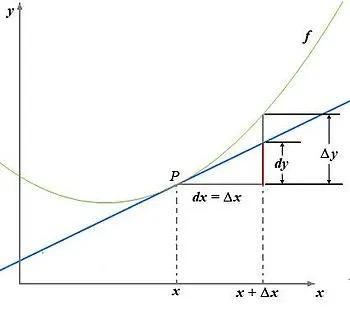
导数的定义:
$$
f’(x) = \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x\to0} \frac{f(x_0+\Delta x) - f(
x_0)}{\Delta x}
\tag{1}
$$
反映的是函数$y=f(x)$在某一点处沿x轴正方向的变化率。再强调一遍,是函数$f(x)$在x轴上某一点处沿着$x$轴正方向
的变化率/变化趋势。直观地看,也就是在$x$轴上某一点处,如果$f’(x)>0$,说明$f(x)
$的函数值在$x$点沿$x$轴正方向是趋于增加的,也就是$x$与$y$是正相关;如果$f’(x)<0$,说明$f(x)
$的函数值在$x$点沿$x$轴正方向是趋于减少的,也就是$x$与$y$是负相关。
这里补充上图中的Δy、dy等符号的意义及关系如下:
- $\Delta x$:$x$的变化量;
- $dx$:$x$的变化量$Δx$趋于0时,则记作微元$dx$;
- $Δy$:$Δy=f(x_0+Δx)-f(x_0)$,是函数的增量;
- $dy$:$dy=f’(x_0)dx$,是切线的增量;
当$Δx→0$时,$dy$与$Δy$都是无穷小,$dy$是$Δy$的主部,即$Δy=dy+o(Δx)$.
导数和偏导数
偏导数的定义如下:
$$
\frac{\partial}{\partial x_j}f(x_0, x_1, \dots, x_n)
= \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}
= \lim_{\Delta x\to0} \frac{f(x_0,\dots, x_j+\Delta x, \dots ,x_n) - f(x_0, \dots , x_j, \dots, x_n)}{\Delta x}
\tag{2}
$$
可以看到,导数与偏导数本质是一致的,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。直观地说,偏导数也就是函数在某一点上沿坐标轴正方向的的变化率,如果有多个元,则坐标轴也有多个。
区别在于:
- 导数,指的是一元函数中,函数$y=f(x)$在某一点处沿$x$轴正方向的变化率;
- 偏导数,指的是多元函数中,函数$y=f(x_1,x_2,…,x_n)$在某一点处沿某一坐标轴$(x1,x2,…,xn)$正方向的变化率。
导数与方向导数:
方向导数的定义如下:
$$
\begin{align}
\frac{\partial}{\partial l}f(x_0, \dots, x_n) &= \lim_{\rho \to 0} \frac{\Delta y}{\Delta x} \\
&= \lim_{\rho \to 0}\frac{f(x_0+\Delta x_0, \dots, x_j+\Delta x_j, \dots, x_n+\Delta x_n) - f(x_0, \dots, x_j, \dots,
x_n)}{\rho} \\
其中: \rho &= \sqrt{(\Delta x_0)^2 + \dots + (\Delta x_j)^2 + \dots + (\Delta x_n)^2}
\end{align}
\tag{3}
$$
在前面导数和偏导数的定义中,均是沿坐标轴正方向讨论函数的变化率。那么当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即:某一点在某一趋近方向上的导数值。
通俗的解释是:
我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。
导数与梯度
梯度的定义如下:
$$
grad\ f(x_0, x_1,\dots,x_n) = \left( \frac{\partial f}{\partial x_0},\dots, \frac{\partial f}{\partial x_,}, \dots,
\frac{\partial f}{\partial x_n}\right)
\tag{4}
$$
梯度的提出只为回答一个问题:
函数在变量空间的某一点处,沿着哪一个方向有最大的变化率?
梯度定义如下:
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
这里注意三点:
- 梯度是一个向量,即有方向有大小;
- 梯度的方向是最大方向导数的方向;
- 梯度的值是最大方向导数的值。
导数与向量
提问:导数与偏导数与方向导数是向量么?
向量的定义是有方向$(direction)$有大小$(magnitude)$的量。
从前面的定义可以这样看出,偏导数和方向导数表达的是函数在某一点沿某一方向的变化率,也是具有方向和大小的。因此从这个角度来理解,我们也可以把偏导数和方向导数看作是一个向量,向量的方向就是变化率的方向,向量的模,就是变化率的大小。
那么沿着这样一种思路,就可以如下理解梯度:
梯度即函数在某一点最大的方向导数,函数沿梯度方向函数有最大的变化率。
梯度下降法
既然在变量空间的某一点处,函数沿梯度方向具有最大的变化率,那么在优化目标函数的时候,自然是沿着负梯度方向
去减小函数值,以此达到我们的优化目标。
如何沿着负梯度方向减小函数值呢?既然梯度是偏导数的集合,如下:
$$
grad\ f(x_0, x_1,\dots,x_n) = \left( \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1,}, \dots,
\frac{\partial f}{\partial x_n}\right)
\tag{5}
$$
同时梯度和偏导数都是向量,那么参考向量运算法则,我们在每个变量轴上减小对应变量值即可,梯度下降法可以描述如下:
$$
\begin{align}
Repeat \quad \lbrace \\
x_0 & := x_0 - \alpha \frac{\partial f}{\partial x_0} \\
\vdots \\
x_j & := x_j - \alpha \frac{\partial f}{\partial x_j} \\
\vdots \\
x_n & := x_n - \alpha \frac{\partial f}{\partial x_n} \\
\rbrace
\end{align}
\tag{6}
$$
其中:
$\alpha$ 是步长,也就是学习速度。
$:=$ 是赋值操作。
以上就是梯度下降法的由来,大部分的机器学习任务,都可以利用$Gradient\ Descent$来进行优化。
深度学习的数学知识-微积分相关概念

