对机器学习的一点思考
机器学习的定义
通常情况下来讲,机器学习有如下几个定义:
- 机器学习是一门人工智能的科学,该领域的主要研究对象是人工智能,特别是如何在经验学习中改善具体算法的性能。
- 机器学习是对能通过经验自动改进的计算机算法的研究。
- 机器学习是用数据或以往的经验,以此优化计算机程序的性能标准。
- 一种经常引用的英文定义是:A computer program is said to learn from experience E with respect to some class of tasks T
and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
一般来说,第4种定义是比较流行的,也会被经常定义,简单的来说,就是:
如果一个计算机程序能够做到如下的内容,那么他就是机器学习:几个计算机程序能够学习关于任务$T$的历史经验$E$,从而能够使得度量(如:预测、分类、识别等)其性能的$P$得以提升。
在西瓜书中的定义是:
机器学习正是这样一门学科,它致力于研究如何通过计算的手段,利用经验来改善系统自身的性能。在计算机系统中,“经验”通常以“数据”形式存在,因此,机器学习所研究的主要内容,是关于在计算机上从数据中产生“模型”(model)的算法,即“学习算法”(learning
algorithm)
在数据科学入门中:
创建并使用那些由学习数据而得出的模型。在其他语境中,也可以被叫作预测建模或者数据挖掘。
机器学习的目的
机器学习的目的在我看来,其实就是将我们现实世界中的现象通过各种函数及概率进行拟合,从而能够达到预测的目的,包括:
- 垃圾邮件检测
- 信用卡诈骗检测
- 自动驾驶(路况分析)
- 人脸识别
- 广告(文章、商品等)精准投放
实现方式
从简单的例子开始
在Andrew Ng的课程中,第一个简单的例子就是房价预测,具体的案例是这样的:
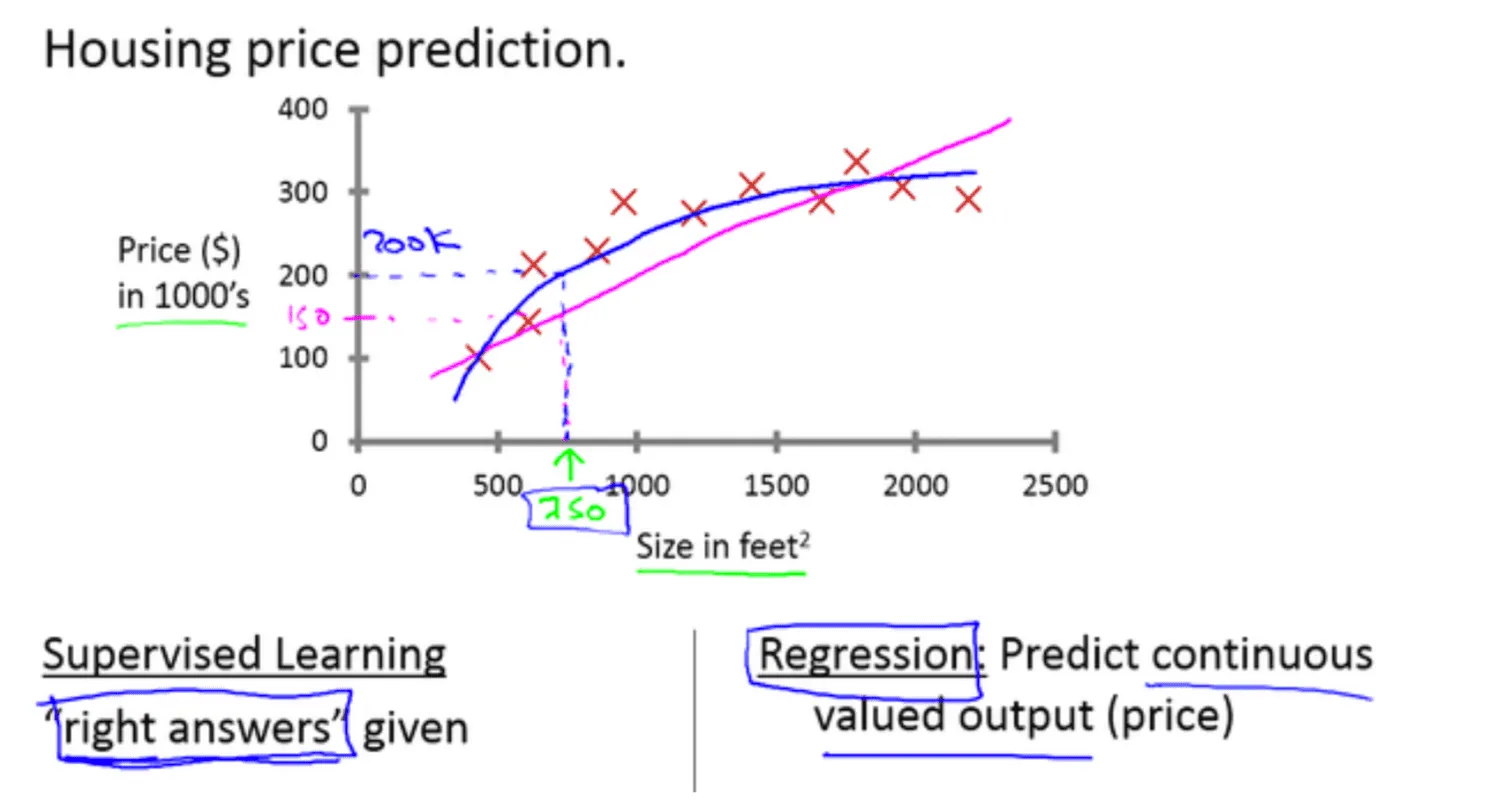
上面的例子进行了一个基本的假设,就是房价只与其面积相关,也就是,房价是一个关于面积的函数值,但是我们不知道这个函数是什么,所以,无法对房价进行预测(关于面积的预测),这时候我们就需要用到机器学习了。
更具经验,我们假设面积与房价的函数关系为:
$$
房价 = f(面积) = \theta_1\times面积 + \theta_2
\tag{1}
$$
一个简单的一元线性方程,我们可以简化为下面的函数:
$$
f(x) = \theta_1x_1+\theta_0x_0
\tag{2}
$$
$2$式中的$\theta$为参数,$x$为特征,一般叫做:$fact$ 或者
$feature$.我们刚刚只说了,房价只与面积有关,为什么这里有个$x_0$呢?这是为了让方程最终可以简化为向量(多个$feature$的情况下为矩阵$Matrix$或者张量$Tensor$),我们令$x_0=1$,则$2$变为:
$$
f(x) = \theta_1x_1+\theta_0x_0 = \left[ \theta_1 \quad \theta_0 \right]
\left[\begin{matrix} x_1 \\ x_0 \end{matrix}\right] = \left[ \theta_1 \quad \theta_0 \right]
\left[\begin{matrix} x_1 \\ 1 \end{matrix}\right]
\tag{3}
$$
我们可以将上式再次简写为:
$$
f(x) \sim \left[ \theta_1 \quad \theta_0 \right]
\tag{4}
$$
假设我们的现实情况就是一个一元线性函数,由于各种原因,我们的样本数据不可能会完全按照一元函数,所以误差是难免的,我们做机器学习训练的时候,目标就是将这种误差减小,使我们的函数尽量你和真实情况。
损失函数
损失函数$(Loss\ Function)$又叫做代价函数$(Cost\ Function)$,一般是值域大于$0$的一个函数,通常来讲,损失函数有以下几种,可以更具经验和实际情况来判断具体使用哪一种:
以下内容来自:https://www.csuldw.com/2016/03/26/2016-03-26-loss-function/
$$
\theta^* = \arg \min_\theta \frac{1}{N}{}\sum_{i=1}^{N} L(y_i, f(x_i; \theta)) + \lambda\ \Phi(\theta)
\tag{5}
$$其中,前面的均值函数表示的是经验风险函数,$L$代表的是损失函数,后面的ΦΦ是正则化项$(regularizer)$或者叫惩罚项(penalty
term),它可以是$L1$,也可以是$L2$,或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的$\theta$值
。下面主要列出几种常见的损失函数。
log对数损失函数(逻辑回归)
有些人可能觉得逻辑回归的损失函数就是平方损失,其实并不是。平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到,而逻辑回归得到的并不是平方损失。在逻辑回归的推导中,它假设样本服从
伯努利分布(0-1分布),然后求得满足该分布的似然函数,接着取对数求极值等等。而逻辑回归并没有求似然函数的极值,而是把极大化当做是一种思想,进而推导出它的经验风险函数为:
**最小化负的似然函数(即$\max F(y,f(x)) \to \min -F(y, f(x))$)**。从损失函数的视角来看,它就成了$log$损失函数了。
log损失函数的标准形式:
$$
L(Y,P(Y|X)) = -\log P(Y|X)
\tag{6}
$$
刚刚说到,取对数是为了方便计算极大似然估计,因为在$MLE$中,直接求导比较困难,所以通常都是先取对数再求导找极值点。损失函数L(Y,
P(Y|X))表达的是样本X在分类Y的情况下,使概率P(Y|X)达到最大值(换言之,*
*就是利用已知的样本分布,找到最有可能(即最大概率)导致这种分布的参数值;或者说什么样的参数才能使我们观测到目前这组数据的概率最大
**)。因为log函数是单调递增的,所以$\log P(Y|X)$也会达到最大值,因此在前面加上负号之后,最大化$P(Y|X)$就等价于最小化$L$了。
逻辑回归的$P(Y=y|x)$表达式如下(为了将类别标签y统一为1和0,下面将表达式分开表示):
$$
P(Y=y|x) = \left\lbrace\begin{matrix}
h_\theta(x) = g(f(x)) = \frac{1}{1 + exp\lbrace - f(x) \rbrace }& ,y=1 \\
1 - h_\theta(x) = 1 - g(f(x)) = \frac{1}{1 + exp\lbrace f(x) \rbrace } & ,y=0
\end{matrix}\right.
\tag{7}
$$
将它带入到上式,通过推导可以得到logistic的损失函数表达式,如下:
$$
L(y,P(Y=y|x)) = \left\lbrace \begin{matrix}
\log (1+exp{-f(x)}) & ,y=1\
\log (1+exp{ f(x)}) & ,y=0\
\end{matrix}\right.
\tag{8}
$$
逻辑回归最后得到的目标式子如下:
$$
J(\theta) = - \frac{1}{m} \sum_{i=1}^m
\left [ y^{(i)} \log h_{\theta}(x^{(i)}) + (1-y^{(i)}) \log(1-h_{\theta}(x^{(i)})) \right ]
\tag{9}
$$
上面是针对二分类而言的。这里需要解释一下:**之所以有人认为逻辑回归是平方损失,是因为在使用梯度下降来求最优解的时候,它的迭代式子与平方损失求导后的式子非常相似,从而给人一种直观上的错觉
**。
平方损失函数(最小二乘法, Ordinary Least Squares )
最小二乘法是线性回归的一种,$OLS$将问题转化成了一个凸优化问题。在线性回归中,它假设样本和噪声都服从高斯分布(为什么假设成高斯分布呢?其实这里隐藏了一个小知识点,就是
中心极限定理,可以参考【central limit theorem】
),最后通过极大似然估计(MLE)可以推导出最小二乘式子。最小二乘的基本原则是:**最优拟合直线应该是使各点到回归直线的距离和最小的直线,即平方和最小
**。换言之,$OLS$是基于距离的,而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢(即$Mean
squared error, MSE$),主要有以下几个原因:
- 简单,计算方便;
- 欧氏距离是一种很好的相似性度量标准;
- 在不同的表示域变换后特征性质不变。
平方损失($Square\ loss$)的标准形式如下:
$$
L(Y, f(X)) = (Y - f(X))^2
\tag{10}
$$
当样本个数为n时,此时的损失函数变为:
$$
L(Y, f(X)) = \sum _{i=1}^{n}(Y - f(X))^2
\tag{11}
$$
$Y-f(X)$ 表示的是残差,整个式子表示的是残差的平方和,而我们的目的就是最小化这个目标函数值(注:该式子未加入正则项),也就是最小化残差的平方和$(residual
sum of squares,RSS)$。
而在实际应用中,通常会使用均方差$(MSE)$作为一项衡量指标,公式如下:
$$
MSE = \frac{1}{n} \sum_{i=1} ^{n} (\tilde{Y_i} - Y_i )^2
\tag{12}
$$
上面提到了线性回归,这里额外补充一句,我们通常说的线性有两种情况,一种是因变量y是自变量x的线性函数,一种是因变量y是参数αα的线性函数。在机器学习中,通常指的都是后一种情况。
指数损失函数(Adaboost)
学过$Adaboost$算法的人都知道,它是前向分步加法算法的特例,是一个加和模型,损失函数就是指数函数。在$Adaboost$中,经过$m$次迭代之后,可以得到$f_m(
x)$:
$$
f_m (x) = f_{m-1}(x) \alpha_m G_m(x)
\tag{13}
$$
$Adaboost$每次迭代时的目的是为了找到最小化下列式子时的参数$\alpha$ 和$G$:
$$
\arg \min_{\alpha, G} = \sum_{i=1}^{N} exp[-y_{i} (f_{m-1}(x_i) \alpha G(x_{i}))]
\tag{14}
$$
而指数损失函数$(exp-loss)$的标准形式如下
$$
L(y, f(x)) = \exp[-yf(x)]
\tag{15}
$$
可以看出,Adaboost的目标式子就是指数损失,在给定n个样本的情况下,Adaboost的损失函数为:
$$
L(y, f(x)) = \frac{1}{n}\sum_{i=1}^{n}\exp[-y_if(x_i)]
\tag{16}
$$
关于$Adaboost$的推导,可以参考Wikipedia:AdaBoost或者《统计学习方法》P145.
Hinge损失函数$(SVM)$
在机器学习算法中,$hinge$损失函数和$SVM$是息息相关的。在线性支持向量机中,最优化问题可以等价于下列式子:
$$
\min_{w,b} \ \sum_{i}^{N} [1 - y_i(w\cdot x_i b)]_{ } \lambda||w||^2
\tag{17}
$$
下面来对式子做个变形,令:
$$
[1 - y_i(w \cdot x_i b)] = \xi_{i}
\tag{18}
$$
于是,原式就变成了:
$$
\min_{w,b} \ \sum_{i}^{N} \xi_i \lambda||w||^2
\tag{19}
$$
如若取$\lambda = \frac{1}{2C}$,式子就可以表示成:
$$
\min_{w,b} \frac{1}{C}\left ( \frac{1}{2}\ ||w||^2 + C \sum_{i}^{N} \xi_i\right )
\tag{20}
$$
可以看出,该式子与下式非常相似:
$$
\frac{1}{m} \sum_{i=1}^{m} l(w \cdot x_i b, y_i) ||w||^2
\tag{21}
$$
前半部分中的$\ l\ $就是hinge损失函数,而后面相当于$L2$正则项。
Hinge 损失函数的标准形式
$$
L(y) = \max(0, 1-y\tilde{y}), y=\pm 1
\tag{22}
$$
可以看出,当$\ |y| \ge 1\ $时,$L(y)=0$。
更多内容,参考Hinge-loss。
补充一下:在$libsvm$中一共有$4$中核函数可以选择,对应的是$-t$参数分别是:
- 0-线性核;
- 1-多项式核;
- 2-RBF核;
- 3-sigmoid核。
其它损失函数
除了以上这几种损失函数,常用的还有:
0-1损失函数
$$
L(Y, f(X)) = \left\lbrace \begin{matrix}1 ,& Y \neq f(X)\ 0 ,& y = f(X) \end{matrix}\right.
\tag{23}
$$
绝对值损失函数
$$
L(Y, f(X)) = |Y-f(X)| \tag{24}
$$
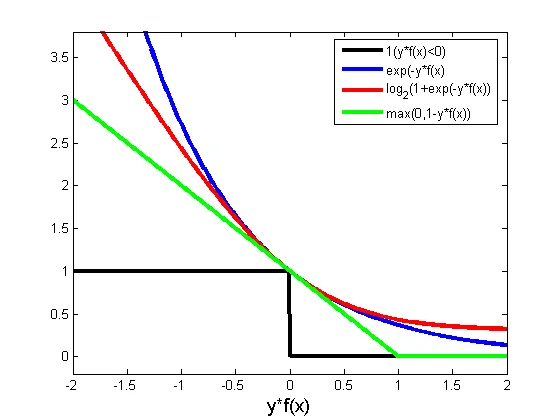
下面来看看几种损失函数的可视化图像,对着图看看横坐标,看看纵坐标,再看看每条线都表示什么损失函数,多看几次好好消化消化。
参数越多,模型越复杂,而越复杂的模型越容易过拟合。

