机器学习之线性回归模型

高斯分布

高斯分布的概率密度函数

$$
f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^ {-\frac{(x-\mu)^2}{2 \sigma^2}}
\tag{1}
$$

记做：
$$
X \sim N(\mu , \sigma ^ 2)
\tag{2}
$$
其函数图像为：

可以看出，正态分布的数学期望值或期望值$\mu$等于位置参数，决定了分布的位置；其方差$\sigma^2$的开平方或这说标准差$\sigma$（标准差的平方等于方差）等于尺度参数，决定了分布的幅度。

以上图像的Python代码

import numpy as np
from bokeh.layouts import row, widgetbox
from bokeh.models import CustomJS, Slider
from bokeh.plotting import figure, output_file, show, ColumnDataSource

N = 100
x = np.linspace(-5.0, 5.0, N)
mu = 0
sigma = 3
s = (1 / (sigma * np.sqrt(2 * np.pi))) \
    * np.exp(- (np.power(x - mu, 2) / (2 * sigma ** 2)))
source = ColumnDataSource(data=dict(x=x, y=s))
plot = figure(y_range=(-0.1, 0.4), x_range=(-5, 5), plot_width=400, plot_height=400)
plot.line('x', 'y', source=source, line_width=3, line_alpha=0.6)
callback = CustomJS(args=dict(source=source),
                    code="var data = source.data;"
                         "var mu = mu.value;"
                         "var sigma = sigma.value;"
                         "x = data['x'];"
                         "y = data['y'];"
                         "console.log(123);"
                         "for (i = 0; i < x.length; i++) {"
                         "y[i] = (1 / (sigma * Math.sqrt(2 * Math.PI))) * Math.exp(- "
                         "(Math.pow(x[i] - mu, 2) / (2 * sigma * sigma)));"
                         "}"
                         "source.change.emit();")
sigma_slider = Slider(start=0.1, end=10, value=3, step=.1,
                      title="标准差(σ)", callback=callback)
callback.args["sigma"] = sigma_slider

mu_slider = Slider(start=-3, end=3, value=0, step=.1,
                   title="期望(μ)", callback=callback)
callback.args["mu"] = mu_slider
layout = row(
    plot,
    widgetbox(sigma_slider, mu_slider),
)
output_file("../output/html/04/slider.html", title="正态分布概率密度函数")
show(layout)

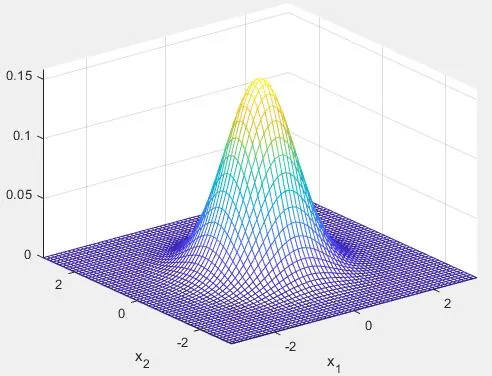
二维高斯分布概率密度函数

$$
f(x,y) = \left ( 2 \pi \sigma_1\sigma_2 \sqrt{1-\rho^2} \right)^{-1}
\exp{\left \lbrace - \frac{1}{2(1-\rho^2)}
\left [ \frac{(x - \mu_1)^2}{\sigma_1^2} - \frac{2\rho(x-\mu_1)(x-\mu_2)}{\sigma_1 \sigma_2} + \frac{(x - \mu_2)^2}{\sigma_2^2} \right]
\right \rbrace }
\tag{3}
$$

其中$\mu_1,\mu_2,\sigma_1,\sigma_2,\rho$都是常数，$x$是自变量，我们称作$X_1,X_2$服从参数为$\mu_1,\mu_2,\sigma_1,\sigma_2,\rho$的二维正态分布，常把这个分布记作：
$$
(X_1,X_2) \sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\tag{4}
$$
的范围分别为：
$$
\begin{align}
\\ - \infty \lt & \mu_1 \lt + \infty
\\ - \infty \lt & \mu_2 \lt + \infty
\\ -1 \lt & \rho \lt 1
\\ \sigma_1 & \ge 0
\\ \sigma_2 & \ge 0
\end{align} \tag{4.1}
$$
其函数图像为：

最大似然估计(MLE)

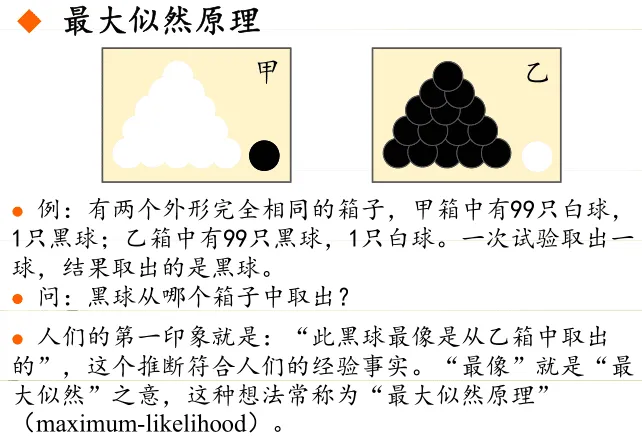
注：最大似然估计在我看来就是，将在先验经验中出现的最多的分类结果作为分类依据。

比如说，有十张照片，都是狗狗，这个是先验经验，我们从中抽取出一种特征：两个眼睛，与之关联起来之后，我们可以说：两个眼睛~狗

但是在继续训练的时候，我们发现，猫也有两个眼睛，这会造成分类错误，所以添加更多的特征，比如：会汪汪叫。结果，发现这个正确概率率提高了不少，除了少数误差数据，比如鹦鹉学舌、人声之类的。我们几乎可以肯定（两个眼睛,
汪汪叫）~ 狗。

注：正确理解正确率的含义，就是正确的概率。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

数学表述

由于样本集中的样本都是独立同分布，可以只考虑一类样本集$D$，来估计参数向量$\theta$。记已知的样本集为：
$$
D = \lbrace x_1, x_2, \dots, x_N \rbrace
\tag{5}
$$
似然函数（$linkehood \quad function$）：联合概率密度函数$p(D|\theta)$称为相对于$\lbrace x_1, x_2, \dots, x_N
\rbrace$的$\theta$的似然函数。
$$
l(\theta) = p(D| \theta) = p(x_1,x_2,\dots,x_N) = \prod_{i=1}^N p(D|\theta)
\tag{5}
$$
如果$\hat{\theta}$是参数空间中能使似然函数$l(\theta)$最大的θ值，则$\hat{\theta}$应该是“最可能”
的参数值，那么$\hat{\theta}$就是$\theta$的极大似然估计量。它是样本集的函数，记作：
$$
\hat{\theta} = d(x_1,x_2,\dots, x_N)=d(D)
\tag{6}
$$
其中，$\theta(x_1,x_2,\dots, x_N)$称作极（最）大似然估计函数的估计值。

最小二乘法

以下来自维基百科

某次实验得到了四个数据点:$ (1,6),(2,5),(3,7),(4,10)$。我们希望找出一条和这四个点最匹配的直线$y=\theta_1 + \theta_2
x$，即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的$\beta_1$和$\beta_2$：

应为有四组数据，我们可以将方程组表达为：
$$
y = \theta_0x_0 + \theta_1 x _1 \\
\tag{7.1}
$$

$$
y = \theta x
\tag{7.2}
$$

$7.2$是$7.1$的向量表示方法。

在例子中，我们的方程组为：
$$
\begin{align}
x_1 + x_2 & = 6 \\
x_1 + 2x_2 & = 5 \\
x_1 + 3x_2 & = 6 \\
x_1 + 4x_2 & = 10 \\
\end{align}
\tag{8}
$$
表达为向量：
$$
\left [
\begin{matrix}
1 & 1 \\
1 & 2 \\
1 & 3 \\
1 & 4
\end{matrix}
\right] \left [
\begin{matrix}
x_1 \\
x_2
\end{matrix}
\right ] = \left[
\begin{matrix}
6 \\
5 \\
7 \\
10
\end{matrix}
\right]
\tag{9}
$$
最小二乘法采用的手段是尽量使得等号两边的方差最小，也就是找出下面这个函数的最小值：
$$
S(\beta_1, \beta_2) = [6-(\beta_1 + \beta_2)]^2 + [5-(\beta_1 + 2\beta_2)]^2 +
[7-(\beta_1 + 3\beta_2)]^2 + [10-(\beta_1 + 4\beta_2)]^2 \tag{10}
$$

对于我们的拟合曲线来说，上面的方差函数就是我们所说的损失函数的一种。其中的每一项，如$6-(\beta_1+\beta_2)
$就是其偏差。为防止正负偏差互相抵消，所以对其进行平方操作，然后求所有偏差之和的最小值，就是拟合最好的情况，

对两边分别求两个参数的偏导数：
$$
\frac{\partial S }{\partial\beta_1} = 0 = 8\beta_1 + 20 \beta_2 + 56 \\
\frac{\partial S}{\partial \beta_2} = 0 = 20\beta_1 + 60\beta_2 + 154
\tag{11}
$$
求解方程组，得到：
$$
\beta_1 = 3.5 \\
\beta_2 = 1.4
\tag{12}
$$
如此就得到了一个只有两个未知数的方程组，很容易就可以解出：根据结论。最小值可以通过对$S(\beta_1, \beta_2)
$分别求$\beta_1$和$\beta_2$的偏导数偏导数)，然后使它们等于零得到。

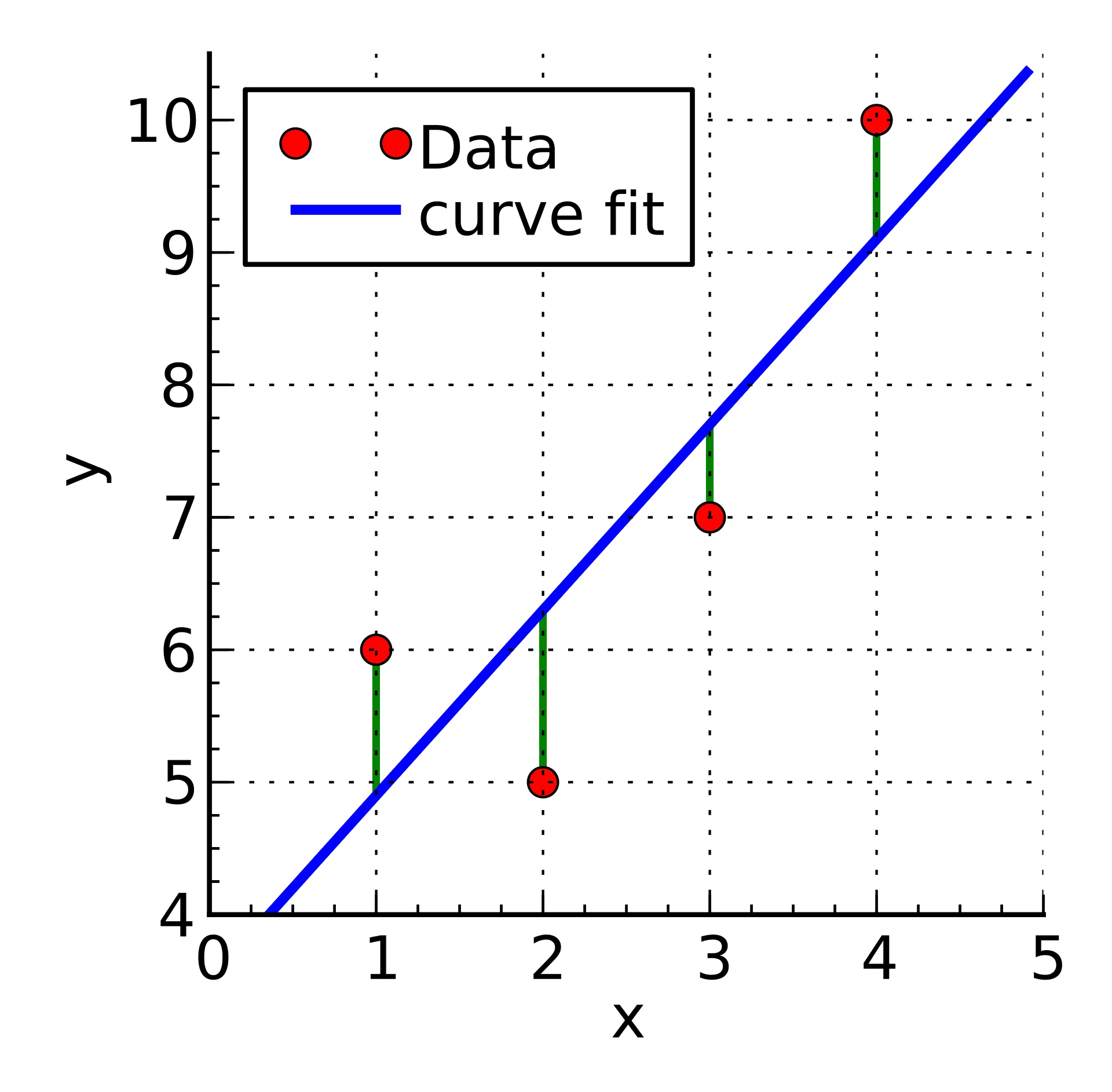
也就是说直线$y=3.5 + 1.4 x$ 是最佳的。

$Logistic$回归

$Sigmoid$函数

$Sigmoid$函数其实是将整个实数轴上的所有实数全部映射到$0 \sim 1$之间，即：$[- \infty, + \infty] \sim [0,1]$，在绝对值很大的时候，会将其映射的值贴近与0或者1。

$Logestic$ 回归

$Logestic$回归的假设函数如下：
$$
\begin{align}
h_\theta（x）& = g(\theta^T x) \\
g(z) & = \frac{1}{1+e^{-z}}
\end{align}
\tag{13}
$$
将其合并为一个公式：
$$
h_\theta = \frac{1}{1+e^{-\theta ^T x}}
\tag{14}
$$
其中$x$是我们的输入，$\theta$为我们要求取的参数。

一个机器学习的模型，实际上是把决策函数限定在某一组条件下，这组限定条件就决定了模型的假设空间。当然，我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是：
$$
P( y = 1 | x;\theta) = g(\theta ^Tx) = \frac{1}{1+e^{-\theta ^Tx}}
\tag{15}
$$
这个函数的意思就是在给定$x$和$\theta$的条件下$y=1$的概率。

这里$g(h)$就是我们上面提到的$sigmoid$函数，与之相对应的决策函数为：
$$
y^* = 1, ifP(y=1|x) \gt 0.5
\tag{16}
$$
选择$0.5$作为阈值是一个一般的做法，实际应用时特定的情况可以选择不同阈值，如果对正例的判别准确性要求高，可以选择阈值大一些，对正例的召回要求高，则可以选择阈值小一些。

梯度下降算法

$$
\Theta^1 = \Theta^0 - \alpha \nabla J (\Theta) \\
evaluated \quad at \quad \Theta^0
\tag{17}
$$

此公式的意义是：$J$是关于$\Theta$的一个函数，我们当前所处的位置为$\Theta^0$点，要从这个点走到$J$的最小值点(
此处有可能是极小值二不是最小值)。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是$\alpha$，走完这个段步长，就到达了$\Theta^1$这个点！

损失函数的选择

对于训练样本来说，我们选择了一条曲线：
$$
\hat{y}_i = \theta_0 + \theta_1 x
\tag{18}
$$
作为其拟合曲线。

我们为其构造了一个损失函数：
$$
C = \sum_{i=1}^n (y_i - \hat{y}_i)^2
\tag{19}
$$
表示每个训练数据点$（x_i, y_i）$到拟合直线$\hat{y_i} = \theta_0 + \theta_1
x$的竖直距离的平方和，通过最小化这个损失函数来求得拟合直线的最佳参数$\mathbb{\theta}$，实际上就是求损失函数$C$在取得最小值情况下$\mathbb{\theta}$的值。
那么损失函数为什么要用平方差形式呢，而不是绝对值形式，一次方，三次方，或四次方形式？

简单的说，是因为使用平方形式的时候，使用的是“最小二乘法”
的思想，这里的“二乘”指的是用平方来度量观测点与估计点的距离（远近），“最小”指的是参数值要保证各个观测点与估计点的距离的平方和达到最小。

我们设观测输出与预估数据之间的误差为：

$$
{\varepsilon _i} = {y_i} - {\widehat y_i}
\tag{20}
$$

我们通常认为 $\varepsilon$ 服从正态分布，即：
$$
f(\varepsilon _i;u,\sigma ^2) = \frac{1}{\sigma \sqrt {2\pi } }\bullet \exp
\left [ - \frac{(\varepsilon _i - u)^2}{2{\sigma ^2}} \right ]
\tag{21}
$$

我们求的参数$\varepsilon$的极大似然估计$(\mu, \sigma^2)$，即是说，在某个$(\mu, \sigma^2)
$下，使得服从正态分布的$\varepsilon$取得现有样本$\varepsilon$的概率最大。那么根据极大似然估计函数的定义，令：

$$
L(\mu,\sigma^2)=\prod_{i=1}^n \frac{1}{\sqrt{2 \pi}\sigma} \bullet \exp{(-\frac{(\varepsilon_i - \mu)^2}{2 \sigma^2})}
\tag{22}
$$

取对数似然函数：
$$
\log L(\mu, \sigma^2) = -\frac{n}{2} \log \sigma^2 - \frac{n}{2} \log 2 \pi - \frac{\sum_{i=1}^n (\varepsilon_i - \mu)
^2}{2 \sigma^2}
\tag{23}
$$

分别求$(\mu, \sigma^2)$的偏导数，然后置$0$，最后求得参数$(\mu, \sigma^2)$的极大似然估计为：

$$
\mu = \frac{1}{n} \sum_{i=1}{n} \varepsilon_i
\tag{24}
$$

$$
\sigma ^ 2 = \frac{1}{n} \sum_{i=1}^n (\varepsilon_i - \mu) ^ 2
\tag{25}
$$

我们在线性回归中要求得最佳拟合直线$\hat{y_i} = \theta_0 + \theta _ 1
x$，实质上是求预估值$\hat{y_i}$与观测值$y_i$之间的误差$\varepsilon$最小（最好是没有误差）的情况下$\theta$的值。而前面提到过，$\varepsilon$是服从参数$(
\mu, \sigma^2)$的正态分布，那最好是均值$\mu$和方差$\sigma$趋近于$0$或越小越好。即:

$$
\mu = \frac{1}{n} \sum_{i=1}^n \varepsilon_i = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i) \to 0 (越小越好)
\tag{26})
$$

$$
\sigma ^2 = \frac{1}{n} \sum_{i = 1}^n (\varepsilon_i - \mu)^2 = \frac{1}{n} \sum_{i=1}^n (y_i - \widehat y_i - \mu)^2
\approx \frac{1}{n} \sum _{i = 1}^n (y_i - \widehat{y_i})^2
\tag{27}
$$
而这与最前面构建的平方形式损失函数本质上是等价的。