神经网络中，梯度下降算法的具体实现原理

本文主要讲解误差逆传播算法的实现。

BP网络

在将单层感知器转换为多层神经网络之后，其损失函数可以使用下面的军方误差的形式去表示，具体如下：

$$
E_k = \frac{1}{2} \sum_{j=1}^{l} (\hat{y}_j^k - y_j^k)^2
\tag{1}
$$

上面公式中的主要几个变量的含义如下：

• $\hat{y}_j^k$表示，在第$j$个样本上的预测值，也就是神经网络在第$k$层的输出，如果这个$k$是最后一层，一般就是最后的预测结果。

• $y_j^k$表示，在第$j$个样本上的真实值。

使二者的均方误差最小，就是神经网络训练过程的主要任务。

其中$\hat{y}_j^k$的计算公式为：

$$
\hat{y}_j^k = f(\beta_j - \theta_j)
\tag{2}
$$

• $\beta_j$表示第$j$个神经元接收到的输入信号，一般为$\beta_j = \sum_{h=1}^q w_{h,j}b_h$.

• $\theta_j$表示第$j$个神经元的激活阈值。

• $f$函数是一个激活函数，一般使用$Sigmoid$函数。

$Sigmoid$函数有一个神奇的特性，就是求导后可以简化：

$$
f’(x) = f(x)(1-f(x)),
\tag{3}
$$

具体推导：

\begin{align} Sigmoid(x) & = \frac{1}{1+e^{-x}} \\ \frac{d Sigmoid(x)}{d x} & = \frac{d \frac{1}{1 + e^{-x}}}{d x} \\ & = \frac{e^{-x}}{({1+e^{-x}})^2} \\ & = \frac{1 + e^{-x} - 1}{({1+e^{-x}})^2} \\ & = \frac{1 + e^{-x} - 1}{({1+e^{-x}}) \bullet ({1+e^{-x}})} \\ & = \frac{1}{({1+e^{-x}})} \bullet \frac{1 + e^{-x} - 1}{({1+e^{-x}})} \\ & = \frac{1}{({1+e^{-x}})} \bullet \left [ 1 + \frac{- 1}{({1+e^{-x}})} \right ]\\ & = Sigmod(x) \bullet (1 - Sigmoid(x)) \end{align} \tag{4}

• $w_{h,j}$为隐藏层$h$到输出层第$j$个神经元的连接权重，这正是我们需要去优化的参数

• $b_h$为隐藏层第$h$个神经元的输出。

再向前推一步，隐藏层的第$h$个神经元的输入为$\alpha_h = \sum_{i=1}^d v_{i,h}x_i$。

• $v_{i,h}$为输入层到隐藏层第$h$个神经元的链接权重。

• $x_i$为输入值。

即，如下图所示：

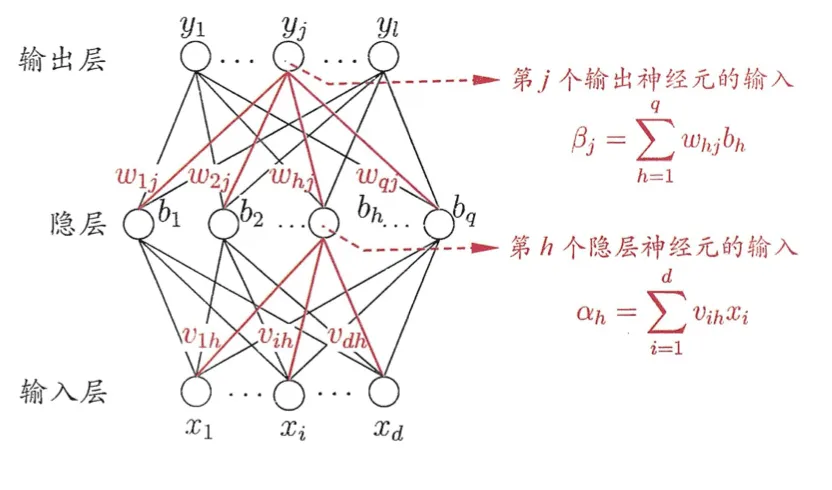
这样，我们就有了输入层到输出层的函数关系链。

我们要想在最后一层，即隐藏层到输出层的损失函数取值最小，则我们需要计算$E_k$对$w_{h,j}$的梯度，并使其最小。

$$
\frac{\partial E_k}{\partial w_{h,j}} = \frac{\partial E_k}{\partial \hat{y}j^k} \bullet \frac{\partial \hat{y}
j^k}{\partial \beta_j} \bullet \frac{\partial \beta_j}{\partial w_{h,j}}
\tag{5}
$$

重新定义一个中间变量，叫做$g_j$:

$$
\begin{aligned}
g_j & = - \frac{\partial E_k}{\partial \hat{y}_j^k} \bullet \frac{\partial \partial \hat{y}_j^k }{\partial \beta_j} \\
& = -(\hat{y}_j^k - y_j^k)\bullet f’(\beta_j - \theta_j) \\
& = \hat{y}_j^k (1-\hat{y}_j^k)(y_j^k -\hat{y}_j^k)
\end{aligned}
\tag{6}
$$

则：

$$
\begin{aligned}
\Delta w_{hj} & = - \eta \frac{\partial E_k}{\partial w_{hj}} \\
& = - \eta g_j \frac{\partial \beta_j}{\partial w_{hj}} \\
& = \eta g_j b_h
\end{aligned}
\tag{7}
$$

类似可以得到：

$$
\Delta \theta_j = - \eta g_j
\tag{8}
$$

$$
\Delta v_{ih} = \eta e_h x_i
\tag{9}
$$

$$
\Delta \gamma_h = - \eta e_h
\tag{10}
$$

上述式子中，$e_h$为：

$$
\begin{aligned}
e_h & = - \frac{\partial E_k}{\partial \alpha_h} \\
& = - \frac{\partial E_k}{\partial b_h} \bullet \frac{\partial b_h}{\partial \alpha_h} \\
& = - \sum_{i=1}^l \frac{\partial E_k}{\partial \beta_j} \bullet \frac{\partial \beta_j}{\partial b_h} f’(\alpha_h -
\gamma_h) \\
& = \sum_{i=1}^l w_{hj}g_j f’(\alpha_h - \gamma_h) \\
& = b_h(1- b_h)\sum_{j=1}^l w_{hj}g_j
\end{aligned}
\tag{11}
$$

反向传播算法的核心就是通过后面一层去调整前一层，一直到输入层的过程，主要是为了简化计算量，有的放矢，而不是完全的随机去猜参数。